Il teorema di Cramer
Il teorema di Cramer calcola la soluzione del sistema lineare quando la matrice dei coefficienti A è una matrice quadrata e il determinante det(A) è diverso da zero.
Perché il teorema di Cramer non è applicabile se il determinante è nullo? Se il determinante det(A)=0 allora il rango rg(A)<n. Secondo il teorema di Rouché-Capellì il sistema non ha soluzioni oppure ne ha infinite.
Un sistema di equazioni con n equazioni e n incognite è anche detto sistema creameriano.
$$ \begin{cases} a_{11} x_1 + a_{12}x_2 + ... + a_{1n}x_n = b_1 \\ \vdots \\ a_{n1} x_1 + a_{n2}x_2 + ... + a_{nn}x_n = b_n \end{cases} $$
Come funziona il teorema di Cramer
Esistono due metodi di calcolo alternativi per usare il teorema di Cramer.
Metodo 1
Dato un sistema quadrato ΣB con n equazioni e n incognite, in cui A è la matrice dei coefficienti e B al matrice dei termini noti
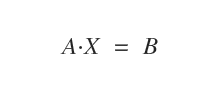
il sistema ammette un'unica soluzione X solo se la matrice quadrata dei coefficienti A del sistema è invertibile.
In tal caso la soluzione è il prodotto tra la matrice inversa A-1 e la matrice dei termini noti B del sistema.
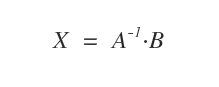
Nota. Una delle precondizioni per risolvere il sistema con il teorema di Cramer è il determinante della matrice dei coefficienti diverso da zero ( det(A)≠0 ), perché una matrice è invertibile se e soltanto se il suo determinante è diverso da zero.
Metodo 2
Il teorema di Cramer può essere applicato anche in un altro modo.
Data una matrice Ci ottenuta sostituendo la i-esima colonna della matrice dei coefficienti A con la matrice dei termini noti B, la soluzione xi è uguale al rapporto tra i determinanti det(Ci)/det(A).
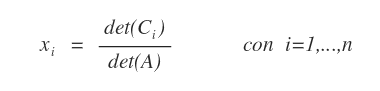
Il calcolo va ripetuto per ogni incognita xi del sistema lineare.
Un esempio pratico
Metodo 1
Provo a calcolare la soluzione del seguente sistema lineare tramite Cramer.
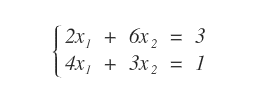
Lo trasformo in forma matriciale
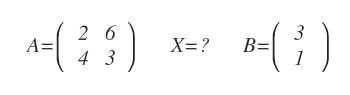
La matrice dei coefficienti A è una matrice quadrata. Quindi posso continuare.
Per verificare se è anche una matrice invertibile calcolo il determinante di A.
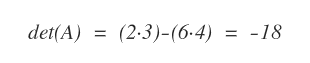
Il determinante della matrice A è diverso da zero. Pertanto, la matrice A è invertibile.
La matrice inversa A-1 è la seguente:
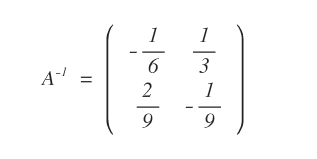
Nota. Per vedere il procedimento di calcolo della matrice invertibile.
Ora per ottenere la soluzione devo calcolare il prodotto delle matrici A-1·B.
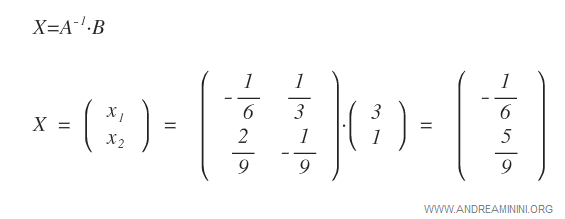
Ho così ottenuto il vettore X con le soluzioni dove x1=-1/6 e x2=5/9.
Metodo 2
Provo a risolvere il sistema lineare anche con il secondo metodo di Cramer.
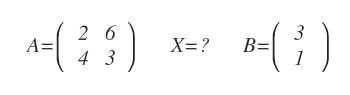
Il determinante della matrice dei coefficienti è
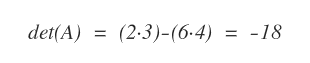
Ora sostituisco la prima colonna della matrice dei coefficienti A con i termini noti B.
Ottengo così la matrice C1.
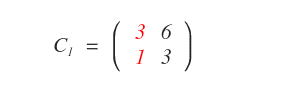
Poi calcolo il determinante di C1.
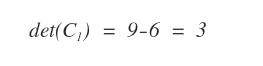
Infine, calcolo il rapporto tra i determinanti det(C1)/det(A).
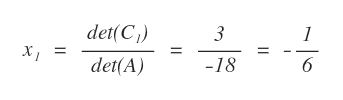
Ho così ottenuto la soluzione dell'incognita x1 ossia x1=-1/6.
Ripeto lo stesso procedimento per calcolare l'altra incognita x2.
Sostituisco la seconda colonna della matrice dei coefficienti A con la colonna dei termini noti B.
Poi calcolo il determinante di C2 e lo divido per il determinante di A.

Ho così ottenuto anche la soluzione dell'incognita x2 ossia x2=5/9.
Le soluzioni del sistema lineare sono x1=1/6 e x2=5/9.
Come usare il teorema di Cramer per i sistemi rettangolari
Il metodo di Cramer può essere usato soltanto se il sistema lineare è quadrato, ossia se la matrice dei coefficienti ha lo stesso numero di righe e colonne.
Non può essere usato nei sistemi lineari rettangolari.
Esempio. Una matrice 3x4 non è compatibile con il metodo di Cramer perché non ha un determinante. Viceversa, una matrice quadrata 3x3 ( 2x2, 4x4, ecc. ) è compatibile il metodo di risoluzione di Cramer.
Tuttavia, il metodo di Cramer può essere utilizzato anche nei sistemi rettangolari quando possono essere trasformati in un sistema quadrato equivalente.
Per approfondimenti sulla trasformazione di una matrice rettangolare in una matrice quadrata, rimando alla lettura del metodo di riduzione di una matrice rettangolare a quadrata e del metodo di eliminazione di Gauss-Jordan.
Sono due metodi alternativi che consentono di usare il teorema di Cramer per risolvere anche i sistemi lineari rettangolari ( non quadrati ).
