Eliminazione del termine misto xy nelle coniche

Per eliminare il termine misto $xy$ in una conica è sufficiente ruotare gli assi di un angolo $\alpha$ tale che $$\tan 2\alpha = \frac{B}{A - C}$$ Dove $A, B, C$ sono i coefficienti dell’equazione generale della conica. Gli angoli di rotazione che soddisfano la condizione sono i seguenti $$ \alpha = \tfrac{1}{2} \arctan \left(\frac{B}{A - C}\right) + \tfrac{k\pi}{2} $$

Si può dimostrare che esiste sempre un angolo di rotazione in grado di far sparire il termine misto xy dall'equazione della conica.

Per trovare l'angolo di rotazione:

1. Identifico i coefficienti (A, B, C) nell’equazione generale della conica: $$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$
2. Applico la formula dell’angolo di rotazione $$ \tan 2\alpha = \frac{B}{A - C} $$

   Nota. Se il denominatore $A - C$ è nullo, la tangente non è definita (l’angolo è verticale). In questo caso particolare la condizione si riduce semplicemente a $$ \cos 2\alpha = 0 \quad \Longrightarrow \quad 2\alpha = \tfrac{\pi}{2} + k\pi $$

3. Calcolo l’angolo di rotazione $ \alpha $ e ne scelgo uno $$ \alpha = \tfrac{1}{2} \arctan \left(\frac{B}{A - C}\right) + \tfrac{k\pi}{2} $$
4. Ruoto gli assi secondo l'angolo $ \alpha $ che ho scelto: $$ \begin{cases} x = x'\cos\alpha - y'\sin\alpha \\ \\ y = x'\sin\alpha + y'\cos\alpha  \end{cases}$$
5. Riscrivo l'equazione della conica e il termine misto $ x'y' $ sparisce.

Esempio pratico

Considero la seguente equazione di una conica con termine misto al suo interno:

$$ 4x^2 + 8xy + 4y^2 + \sqrt{2} x - \sqrt{2} y = 0 $$

In questo caso i coefficienti dell'equazione sono $$ A=4, \ B=8, \ C=4, \ D=\sqrt{2}, \ E=-\sqrt{2}, \ F=0$$

Calcolo l'angolo di rotazione che elimina $xy$ usando la regola:

$$ \tan 2\alpha = \frac{B}{A-C} $$

Qui $A-C=0 $ quindi $ \tan 2\alpha$ non esiste.

In questo caso particolare devo applicare la condizione $ \cos 2\alpha=0$, quindi:

$$ 2\alpha = \arccos 0 $$

$$ 2 \alpha = \frac{\pi}{2}+k\pi $$

$$  \alpha=\frac{\pi}{4}+k\frac{\pi}{2} $$

Scelgo per semplicità l'angolo $\alpha=\frac{\pi}{4}$ e svolgo la rotazione degli assi:

$$ \begin{cases} x = x'\cos\alpha + y'\sin\alpha \\ \\ y = -x'\sin\alpha + y'\cos\alpha \end{cases} $$

$$ \begin{cases} x = x'\cos \frac{\pi}{4} + y'\sin \frac{\pi}{4} \\ \\ y = -x'\sin \frac{\pi}{4} + y'\cos \frac{\pi}{4} \end{cases} $$

Sapendo che $ \cos \frac{\pi}{4} = \frac{\sqrt{2}}{2} $ e $ \sin \frac{\pi}{4} = \frac{\sqrt{2}}{2} $

$$ \begin{cases} x = x' \frac{\sqrt{2}}{2} + y' \frac{\sqrt{2}}{2} \\ \\ y = -x' \frac{\sqrt{2}}{2} + y' \frac{\sqrt{2}}{2} \end{cases} $$

$$ \begin{cases} x = \frac{\sqrt{2}}{2} (x' + y') \\ \\ y =  \frac{\sqrt{2}}{2} ( y' -x' ) \end{cases} $$

Sostituisco i termini $ x $ e $ y $ nell'equazione

$$ 4x^2 + 8xy + 4y^2 + \sqrt{2} x - \sqrt{2} y = 0 $$

Sviluppo i termini quadratici $ 4x^2, 8xy , 4y^2 $ e quelli lineari $ \sqrt{2} x, \sqrt{2} y $

• $ 4x^2 = 4 ( \frac{\sqrt{2}}{2} (x' + y') )^2 =  2x'^2+4x'y'+2y'^2 $
• $ 8xy = 8 ( \frac{\sqrt{2}}{2} (x' + y') ) (  \frac{\sqrt{2}}{2} ( y' -x' ) ) = 4y'^2 -4x'^2 $
• $ 4y^2 =  4 ( \frac{\sqrt{2}}{2} (y' -x') )^2 = 2x'^2-4x'y'+2y'^2 $
• $ \sqrt{2} x = \sqrt{2}  \frac{\sqrt{2}}{2} (x' + y') = x'+y' $
• $ - \sqrt{2} y = - \sqrt{2}  \frac{\sqrt{2}}{2} (y' -x' ) = x'-y' $

Quindi, l'equazione diventa

$$ (2x'^2+4x'y'+2y'^2) + ( 4y'^2 -4x'^2 )  + ( 2x'^2 -4x'y'+2y'^2 ) + (x'+y' ) + (x'-y' ) = 0  $$

$$ 2x'^2+4x'y'+2y'^2 + 4y'^2 -4x'^2  + 2x'^2 -4x'y'+2y'^2 + x'+y' + x'-y'  = 0  $$

$$ x^2 (2-4+2) + y'^2 (2 +4 +2) + x'y' (4-4) + 2x'  = 0  $$

$$ 0 \cdot x^2 + 8 \cdot  y'^2 + 0 \cdot x'y' + 2x' = 0  $$

$$ 8 y'^2 + 2x' = 0  $$

Nel sistema ruotato di $\alpha=\frac{\pi}{4}$ il termine misto $ xy $ è scomparso.

$$ 2x' = - 8 y'^2   $$

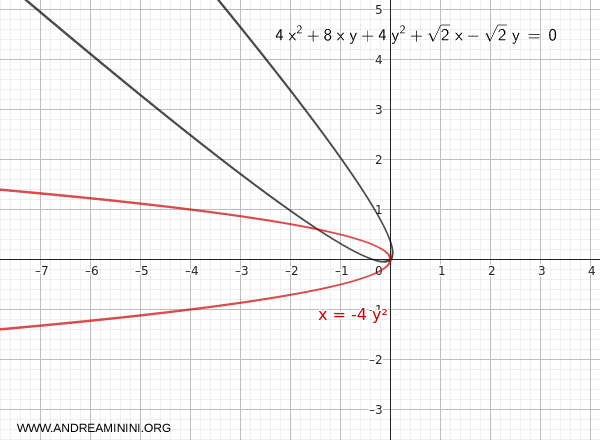
$$ x'=-4 y'^2 $$

Dopo la rotazione la parabola ha il vertice nell’origine, l'asse è parallelo all’asse $x'$ ed è aperta verso sinistra:

La dimostrazione

Considero l'equazione generale di una conica.

$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$

Devo trovare l'angolo $ \alpha $ di una rotazione che annulli il coefficiente $ B $, quello del termine misto $ xy $.

In geometria analitica l'equazione di una rotazione è la seguente:

$$ \begin{cases} x = x'\cos\alpha - y'\sin\alpha \\ y = x'\sin\alpha + y'\cos\alpha  \end{cases}$$

Sostituisco $ x $ e $ y $ nell'equazione della conica.

• Il termine $ Ax^2 $ $$ \begin{aligned} Ax^2 &= A\,(x' \cos \alpha - y' \sin \alpha)^2 \\ &= A\,(x'^2 \cos^2 \alpha - 2x'y' \sin \alpha \cos \alpha + y'^2 \sin^2 \alpha) \end{aligned} $$
• Il termine $ Bxy $ $$ \begin{aligned} Bxy &= B\,(x' \cos \alpha - y' \sin \alpha)(x' \sin \alpha + y' \cos \alpha) \\ &= B\,(x'^2 \cos \alpha \sin \alpha + x'y'(\cos^2 \alpha - \sin^2 \alpha) - y'^2 \sin \alpha \cos \alpha) \end{aligned} $$
• Il termine $ Cy^2 $ $$ \begin{aligned} Cy^2 &= C\,(x' \sin \alpha + y' \cos \alpha)^2 \\ &= C\,(x'^2 \sin^2 \alpha + 2x'y' \sin \alpha \cos \alpha + y'^2 \cos^2 \alpha) \end{aligned} $$
• Il termine $ Dx $ $$ \begin{aligned} Dx &= D\,(x'\cos\alpha - y'\sin\alpha) \\ &= (D\cos\alpha)\,x' + (-D\sin\alpha)\,y' \end{aligned} $$
• Il termine $ Ey $ $$ \begin{aligned} Ey &= E\,(x'\sin\alpha + y'\cos\alpha) \\ &= (E\sin\alpha)\,x' + (E\cos\alpha)\,y' \end{aligned} $$

Ora raccolgo i coefficienti del termini misto $ x'y' $ e li sommo tra loro.

$$ B' = -2A x'y' \sin \alpha \cos \alpha + B x'y' ( \cos^2 \alpha -  \sin^2 \alpha) + 2C x'y' \sin \alpha \cos \alpha $$

$$ B' = x'y' \cdot ( -2A \sin \alpha \cos \alpha + B ( \cos^2 \alpha -  \sin^2 \alpha) + 2C \sin \alpha \cos \alpha ) $$

Per la legge di annullamento del prodotto, il coefficiente $ B' $ del termine misto $ x'y' $ si annulla $ B'=0 $ quando uno dei due fattori è nullo.

Il primo fattore è il caso banale $ x'y'=0 $, quindi mi concentro sul secondo fattore.

$$ - 2A \sin \alpha \cos \alpha + B ( \cos^2 \alpha - \sin^2 \alpha) + 2C \sin \alpha \cos \alpha = 0 $$

Svolgo il raggruppamento parziale

$$ (2C - 2A) \sin \alpha \cos \alpha + B ( \cos^2 \alpha - \sin^2 \alpha) = 0 $$

$$ (C - A) 2 \sin \alpha \cos \alpha + B ( \cos^2 \alpha - \sin^2 \alpha) = 0 $$

In trigonometria secondo le formule di duplicazione $ 2 \sin \alpha \cos \alpha = \sin 2 \alpha $ e $ \cos^2 \alpha - \sin^2 \alpha = \cos 2 \alpha $

$$ (C - A) \sin 2 \alpha + B \cos 2 \alpha = 0 $$

$$ (C - A) \sin 2 \alpha = - B \cos 2 \alpha   $$

Divido entrambi i membri per $ \cos 2 \alpha $

$$ (C - A) \frac{ \sin 2 \alpha }{ \cos 2 \alpha  } = - B   $$

Sapendo che per la seconda relazione fondamentale della trigonometria vale $ \frac{\theta}{\theta} = \tan \theta $

$$ (C - A) \tan 2 \alpha = - B   $$

$$ \tan 2 \alpha = \frac{- B }{C-A }   $$

Moltiplico il secondo membro per $ \frac{-1}{-1} $

$$ \tan 2 \alpha = \frac{- B }{C-A } \cdot \frac{-1}{-1}  $$

$$ \tan 2 \alpha = \frac{ B }{A-C }  $$

Pertanto, quando $ \tan 2 \alpha = \frac{ B }{A-C }  $ si annulla il coefficiente $ B' = 0 $ del termine misto. Ho così dimostrato la condizione di eliminazione del termine misto.

Da qui segue che

$$ 2\alpha = \arctan \left(\frac{B}{A - C}\right) + k\pi, \qquad k \in \mathbb{Z} $$

E quindi:

$$ \alpha = \tfrac{1}{2} \arctan \left(\frac{B}{A - C}\right) + \tfrac{k\pi}{2} $$

In pratica: non esiste un unico $\alpha$, ma una famiglia di angoli che differiscono di $\tfrac{\pi}{2}$.

Per l’eliminazione del termine misto basta sceglierne uno, di solito per semplicità si sceglie quello compreso fra $-\tfrac{\pi}{4}$ e $\tfrac{\pi}{4}$.

E così via.