Sfere di Dandelin

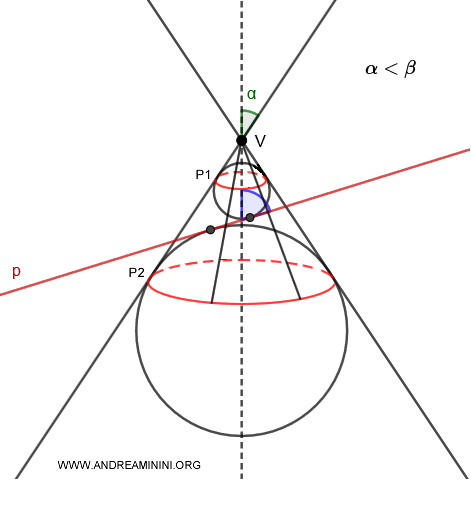
Le sfere di Dandelin sono sfere inscritte in un cono circolare retto a due falde, tangenti a un punto $ F $ di un piano secante $ p $.

Il piano secante $ p $ non deve passare per il vertice V del cono.

A seconda dell'angolo di semiapertura $ \alpha $ del cono e dell'angolo di inclinazione $ \beta $ del piano, ci sono tre possibilità:

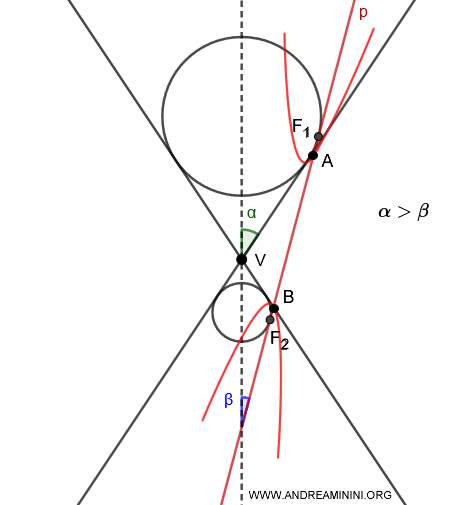
• Se $ \alpha > \beta $ ci sono due sfere di Dandelin inscritte ciascuna in una falda diversa del cono $ p $ e tangenti al piano nei punti $ F_1 $ e $ F_2 $.
  
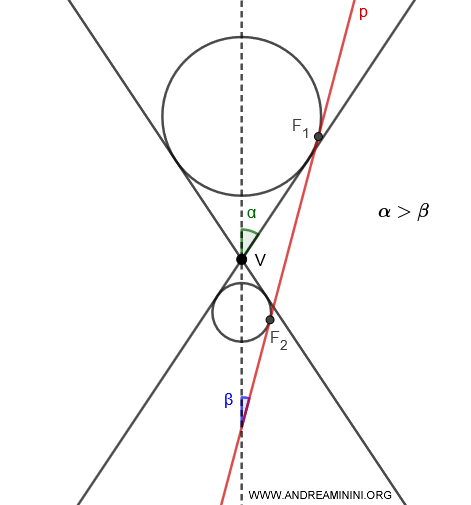
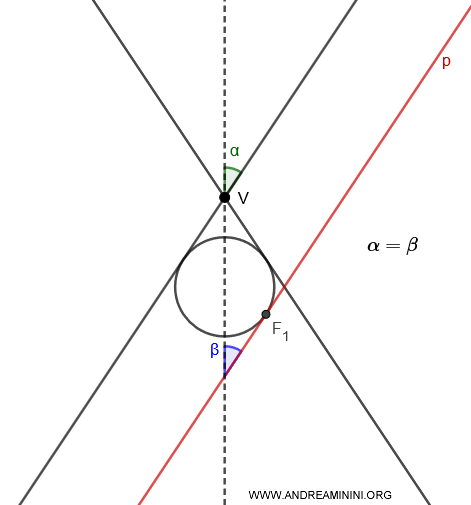
• Se $ \alpha = \beta $ c'è una sola sfera di Dandelin inscritte nella stessa falda intersecata dal piano $ p $.
  
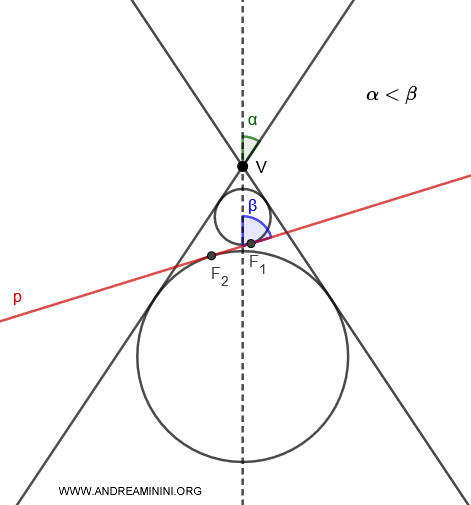
• Se $ \alpha < \beta $ ci sono due sfere di Dandelin inscritte nella stessa falda intersecata dal piano $ p $ e tangenti al piano nei punti $ F_1 $ e $ F_2 $.
  

In questa rappresentazione semplificata il cono circolare e il piano sono visti lateralmente per rendere più comprensibile questo concetto.

In realtà, le sfere di Dandelin sono tangenti a tutte le rette generatrici del cono circolare e i punti di tangenza formano una circonferenza su un piano perpendicolare all'asse del cono.

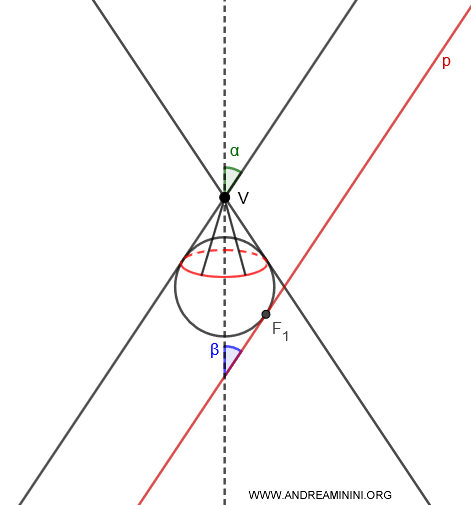
Nota. Le circonferenze si trovano su piani perpendicolari (90°) all'asse di simmetria. Non si trovano sull'asse secante al cono che, invece, è inclinato con un angolazione β.

Date due sfere di Dandelin tangenti alle rette generatrici dello stesso cono, la distanza tra i punti di tangenza $ P_1 $ e $P_2 $ è costante in ciascuna retta genetratrice.

 

Le sfere di Dandelin sono un concetto geometrico, introdotto dal matematico Germinal Pierre Dandelin nel 1822. che viene utilizzato per dimostrare alcune proprietà delle sezioni coniche (ellissi, parabole e iperboli).

Le sezioni coniche (ellisse, parabola, iperbole) sono le curve che si ottengono intersecando questo cono con un piano.

• Ellisse: Quando il piano interseca una falda del cono formando un'ellisse, ci sono due sfere inscritte che toccano il piano della sezione conica in due punti distinti. Questi due punti sono i fuochi dell'ellisse.
• Parabola: Se il piano è parallelo a una generatrice, c'è una sola sfera inscritta che tocca il piano in un punto, che è il fuoco della parabola.
• Iperbole: Quando il piano interseca entrambe le falde del cono, ci sono due sfere inscritte, ognuna delle quali tocca il piano in un punto, che corrispondono ai fuochi dell'iperbole.

Quindi, le sfere di Dandelin forniscono un metodo per dimostrare geometricamente alcune delle proprietà fondamentali delle sezioni coniche, che sono altrimenti trattate con metodi algebrici.

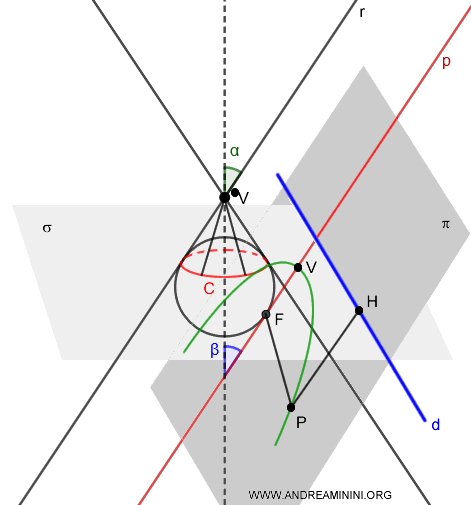
Si può dimostrare che l'eccentricità della conica è determinato dall'angolo di semiapertura $ \alpha $ del cono e dall'angolo di inclinazione $ \beta $ del piano secante.

$$ e = \frac{ \overline{PF} }{ \overline{PH} } = \frac{\cos \alpha }{ \cos \beta} $$

Dove $ \overline{PF} $ è la distanza di un punto  $ P $ della conica dal fuoco $ F $ mentre $ \overline{PH} $ è la distanza del punto $ P $ dalla retta direttrice $ d $.

La retta direttrice $ d $ è l'intersezione del piano secante $ \pi $ con il piano perpendicolare $ \sigma $ all'asse di simmetria del cono.

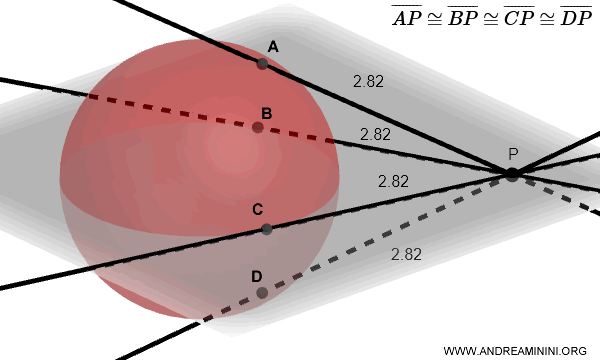
Nota. Un teorema della sfera molto utile nelle dimostrazioni dei teoremi di Dandelin è il seguente: tutti i segmenti tangenti a una sfera condotti da un punto P esterno alla sfera sono tra loro congruenti $ \overline{AP} \cong \overline{BP} \cong \overline{CP} \cong \overline{DP} $

Teorema di Dandelin dell'ellisse

Quando un piano interseca una singola falda di un cono, formando due sfere inscritte che toccano il piano in due punti distinti, $ F_1 $ e $ F_2 $, questi punti rappresentano i fuochi dell'ellisse risultante sul piano. I vertici dell'ellisse, invece, corrispondono ai punti A e B.

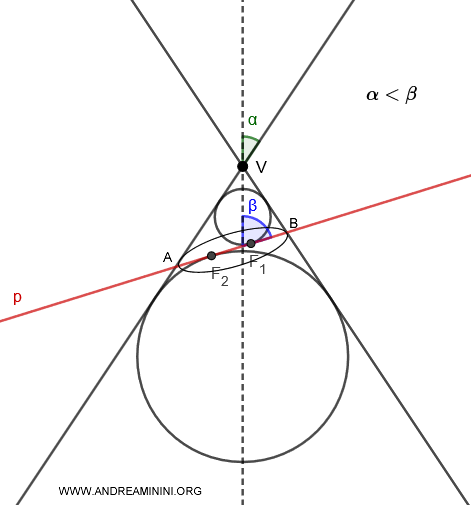
Per ogni punto P dell'ellisse la somma delle distanze $ \overline{PF_1} $ e $ \overline{PF_2} $ è costante ed è uguale alla lunghezza del segmento AB $$ \overline{PF_1} + \overline{PF_2} = \overline{AB} $$

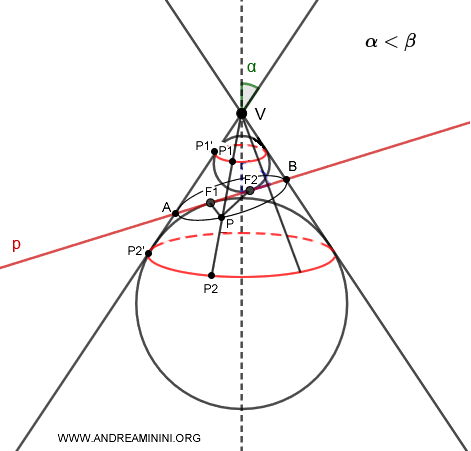
Dimostrazione

I segmenti tra i punti di intersezione delle rette generatrici del cono con le due circonferenze perpendicolari all'asse di simmetria sono congruenti perché provengono da un unico punto esterno V alle sfere.

$$ \overline{P_1P_2} \cong \overline{P_1'P_2'} $$

A sua volta ogni segmento tra le due circonferenze interseca l'ellisse ed è composto dalla somma di due segmenti

$$ \overline{P_1P_2} = \overline{P_1P} + \overline{PP_2} $$

In ogni punto P dell'ellisse la somma delle distanze dai fuochi è costante.

$$ \overline{PF_1} + \overline{PF_2} = k $$

Considero come punto P il vertice A e il vertice B dell'ellisse

$$ \overline{AF_1} + \overline{AF_2}  =  \overline{BF_1} + \overline{BF_2} = k  $$

Devo trovare quanto vale la costante k.

Sapendo che il segmento AB posso scriverlo in questa forma $ \overline{AB} = \overline{AF_2} + \overline{BF_2}  $ deduco che $ \overline{AF_2} = \overline{AB} - \overline{BF_2}  $

$$ \overline{AF_1} + \overline{AF_2}  =  \overline{BF_1} + \overline{BF_2}   $$

$$ \overline{AF_1} + ( \overline{AB} - \overline{BF_2} )  =  \overline{BF_1} + \overline{BF_2}   $$

$$ \overline{AF_1} +  \overline{AB} - \overline{BF_2}   =  \overline{BF_1} + \overline{BF_2}   $$

$$ \overline{AF_1} +  \overline{AB} - \overline{BF_1}   =  \overline{BF_2} + \overline{BF_2}   $$

$$ \overline{AF_1} +  \overline{AB} - \overline{BF_1}   =  2\overline{BF_2}    $$

Il segmento $ \overline{AB} - \overline{BF_1}   = \overline{AF_1} $

$$ \overline{AF_1} +  ( \overline{AB} - \overline{BF_1} )   =  2\overline{BF_2}   $$

$$ \overline{AF_1} +  \overline{AF_1}  =  2\overline{BF_2}    $$

$$ 2 \overline{AF_1}  =  2\overline{BF_2}    $$

Divido entrambi i lati dell'equazione per due

$$  \overline{AF_1}  =  \overline{BF_2}    $$

In questo modo ho dimostrato che i segmenti $  \overline{AF_1}  =  \overline{BF_2}    $ sono congruenti.

A questo punto torno all'equazione precedente dove $ k $ è ancora un valore incognito

$$ \overline{AF_1} + \overline{AF_2}  =  \overline{BF_1} + \overline{BF_2} = k  $$

Sapendo che il segmento $ \overline{AF_2}  = \overline{AF_1} + \overline{F_1F_2} $

$$ \overline{AF_1} + (\overline{AF_1} + \overline{F_1F_2})  =  \overline{BF_1} + \overline{BF_2} = k  $$

$$ \overline{AF_1} + \overline{AF_1} + \overline{F_1F_2}  =  \overline{BF_1} + \overline{BF_2} = k  $$

So già che $  \overline{AF_1}  =  \overline{BF_2}    $

$$ \overline{AF_1} + \overline{BF_2} + \overline{F_1F_2}  =  \overline{BF_1} + \overline{BF_2} = k  $$

La somma dei segmenti $ \overline{AF_1} + \overline{F_1F_2} + \overline{BF_2} = \overline{AB} $

$$ \overline{AB}  =  \overline{BF_1} + \overline{BF_2} = k  $$

Pertanto, la costante k è uguale alla lunghezza del segmento AB

$$ k = \overline{AB} $$

Poiché la costante $ k $ è uguale per qualsiasi punto $ P $ ho dimostrato che

$$ \overline{PF_1} + \overline{PF_2} = \overline{AB} $$

E' esattamente ciò che accade in ogni punto di una ellisse.

Teorema di Dandelin della parabola

Quando un piano secante \( \pi \) è parallelo a una retta generatrice del cono \( r \), esiste una sola sfera inscritta nel cono che tocca il piano secante in un singolo punto \( F \). Il punto \( F \) corrisponde al fuoco di una parabola tracciata sul piano \( \pi \).

La retta direttrice \( d \) della parabola si ottiene dall'intersezione del piano secante \( \pi \) con il piano $ \sigma $ perpendicolare all'asse del cono che contiene la circonferenza $ C $ dei punti di tangenza tra la sfera e il cono.

Per ogni punto \( P \) della parabola vale la relazione

$$ \overline{PH} = \overline{PF} $$

dove \( \overline{PH} \) è la distanza tra il punto \( P \) e la sua proiezione \( H \) sulla retta direttrice, mentre \( \overline{PF} \) è la distanza tra il punto \( P \) e il fuoco \( F \) della parabola.

Questo teorema dimostra geometricamente che la definizione della parabola come luogo dei punti equidistanti da un punto fisso, detto fuoco, e da una retta, detta direttrice, può essere derivata dalla costruzione conica.

Dimostrazione

Considero un punto $ P $ qualsiasi della parabola.

Per il punto $ P $ passa una retta generatrice $ g $ del cono che interseca la circonferenza $ C $ nel punto $ T $.

Traccio una circonferenza $ C_2 $ sul piano perpendicolare all'asse di simmetria del cono che passa per il punto $ P $

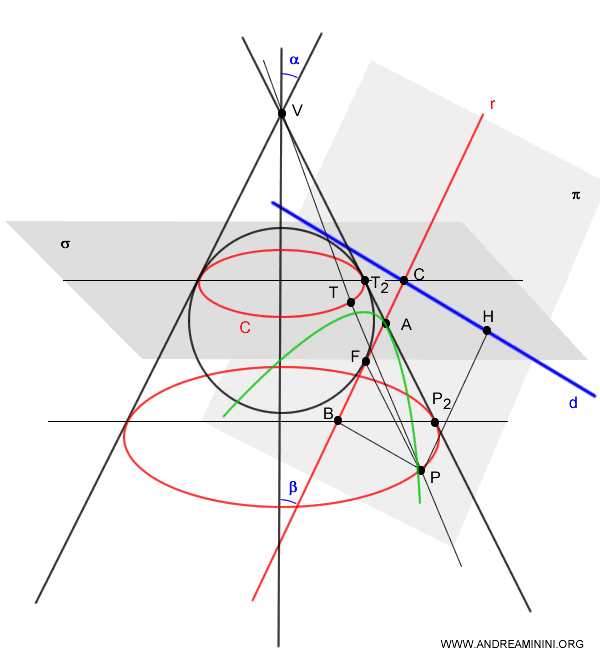
Il segmento $ \overline{PT} $ è congruente con il segmento $ P_2T_2 $ perché le circonferenze $ C $ e $ C_2 $  sono perpendicolari all'asse di simmetria del cono e le rette generatrici hanno tutte lo stesso punto di origine $ V $

$$ \overline{PT} \cong \overline{P_2T_2} $$

Il punto $ B $ è la proiezione del punto $ P $ sull'asse di simmetria $ p $ della parabola mentre il punto $ H $ è la proiezione di  $ P $ sulla retta direttrice $ d $.

Pertanto, il quadrilatero $ CBPH $  è un rettangolo.

I lati opposti di un rettangolo sono tra loro congruenti

$$ \overline{BC} \cong \overline{PH} $$

$$ \overline{BP} \cong \overline{CH} $$

Per ipotesi iniziale l'angolo di semiapertura del cono $ \alpha $ è congruente con l'angolo di inclinazione $ \beta $ del piano secante $ \pi $.

$$ \alpha \cong \beta $$

Pertanto i triangoli $ ACT_2 $ e $ ABP_2 $ sono triangoli simili e isosceli.

Da questo deduco che i segmenti  $ \overline{ P_1T_1 } \cong \overline{BC} $

$$ \overline{ P_1T_1 } \cong \overline{BC} $$

I segmenti $ \overline{PF} $ e $ \overline{PT} $ sono entrambi tangenti alla sfera e hanno origine dallo stesso punto $ P $, quindi sono tra loro segmenti congruenti.

$$ \overline{PF} \cong \overline{PT} $$

Sapendo che $ \overline{PT} \cong \overline{P_1T_1} $ e  $ \overline{P_1T_1} \cong BC $

$$ \overline{PF} \cong \overline{BC} $$

Poiché $ \overline{BC} \cong \overline{PH} $ essendo lati opposti di un rettangolo

$$ \overline{PF} \cong \overline{PH} $$

Questo dimostra che per qualsiasi punto $ P $ della parabola la distanza tra il punto e il fuoco $ F $ è uguale alla distanza tra il punto e la sua proiezione $ H $ sulla retta direttrice $ d $

Nota. Anche nel caso in cui il punto $ P $ è il vertice $ A $ della parabola si conferma la relazione $ PF \cong PH $ in quanto il triangolo $ ACT_2 $ è isoscele, quindi i suoi lati obliqui sono congruenti $ \overline{AC} \cong \overline{AT_2} $. Inoltre, $ \overline{AT_2} \cong \overline{AF} $ in quanto entrambi i segmenti $ \overline{AT_2} $ e $ \overline{AF} $ hanno origine dallo stesso punto $ A $ e sono entrambi tangenti alla sfera. Pertanto, anche quando il punto è $ P=A$ e la sua proiezione è $ H=C $ vale la relazione $ AF \cong AC $ ossia $ PF \cong PH $.

Teorema di Dandelin dell'iperbole

Quando un piano interseca entrambe le falde del cono, esistono due sfere inscritte tangenti al piano secante. I due punti di tangenza sono i fuochi di un'iperbole.

Per ogni punto $ P $ dell'iperbole vale la relazione seguente:

$$ | \overline{PF_1} - \overline{PF_2} | = \overline{AB} $$

Dove $ A $ e $ B $ sono i vertici dell'iperbole.

Dimostrazione

Considero un punto P dell'iperbole che si trova sulla retta generatrice $ g $ del cono.

La retta generatrice interseca le circonferenze $ C_1 $ e $ C_2 $ delle sfere inscritte nei punti $ P_1 $ e $ P_2 $.

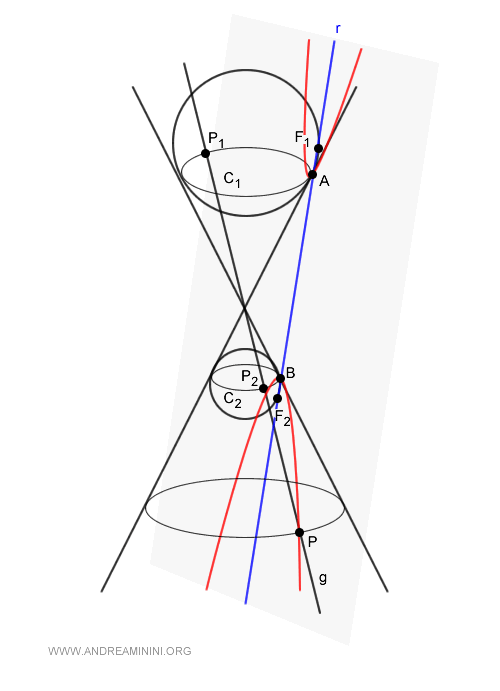
I segmenti $ \overline{PF_1} $ e $ \overline{PP_1} $ sono congruenti perché sono segmenti tangenti a una sfera che hanno origine dallo stesso punto $ P $.

$$ \overline{PF_1} \cong \overline{PP_1} $$

Per la stessa ragione sono congruenti anche i segmenti

$$ \overline{PF_2} \cong \overline{PP_2} $$

Pertanto, anche le loro differenze sono congruenti

$$ | \overline{PF_1} - \overline{PF_2} | = |  \overline{PP_1} -  \overline{PP_2} | $$

La differenza $ |  \overline{PP_1} -  \overline{PP_2} | $ è il segmento $  \overline{P_1P_2} $ che è costante per qualsiasi punto della circonferenza $ C_1 $ o $ C_2 $

$$ | \overline{PF_1} - \overline{PF_2} | = |  \overline{PP_1} -  \overline{PP_2} | = \overline{P_1P_2} $$

Ora prendo come punto $ P $ il vertice $ A $ dell'iperbole

$$ | \overline{AF_1} - \overline{AF_2} | = \overline{P_1P_2}  $$

Poi il vertice $ B $ dell'iperbole

$$ | \overline{BF_2} - \overline{BF_1} |= \overline{P_1P_2}    $$

Entrambe le differenze $ | \overline{AF_1} - \overline{AF_2} | $ e $ | \overline{BF_1} - \overline{BF_2} | $ sono uguali a $ \overline{P_1P_2}  $

$$ | \overline{AF_1} - \overline{AF_2} | =  | \overline{BF_2} - \overline{BF_1} | $$

Il segmento  $ \overline{AF_2} = \overline{F_1F_2} - \overline{AF_1} $ mentre $ \overline{BF_1} = \overline{F_1F_2} - \overline{BF_2} $

$$ | \overline{AF_1} - ( \overline{F_1F_2} - \overline{AF_1} )  | =  | \overline{BF_2} - ( \overline{F_1F_2} - \overline{BF_2} ) | $$

$$ | \overline{AF_1} - \overline{F_1F_2} + \overline{AF_1}   | =  | \overline{BF_2} - \overline{F_1F_2} + \overline{BF_2}  | $$

$$ | 2 \overline{AF_1} - \overline{F_1F_2}    | =  | 2 \overline{BF_2} - \overline{F_1F_2}   | $$

Semplifico l'equazione eliminando $ \overline{F_1F_2} $ da entrambi i lati

$$ | 2 \overline{AF_1}  | =  | 2 \overline{BF_2}  | $$

Sapendo che le lunghezze dei segmenti sono sempre positive elimino i valori assoluti.

$$ 2 \overline{AF_1}  =  2 \overline{BF_2}  $$

Infine, semplifico dividendo per 2 entrambi i lati dell'equazione

$$ \overline{AF_1}  =  \overline{BF_2}  $$

Una volta dimostrata l'uguaglianza $ \overline{AF_1}  =  \overline{BF_2}  $ torno alla differenza $ |  \overline{AF_1} - \overline{AF_2}  | $

$$ |  \overline{AF_1} - \overline{AF_2}  | $$

Sapendo che $ \overline{AF_1}  =  \overline{BF_2}  $

$$ |   \overline{BF_2} - \overline{AF_2}  | $$

Dispongo la differenza in valore assoluto in questa forma equivalente mettendo prima il segmento più lungo

$$ | \overline{AF_2} -  \overline{BF_2}   | $$

La differenza $  \overline{AF_2} -  \overline{BF_2}  $  è il segmento $ \overline{AB} $

$$ | \overline{AF_2} -  \overline{BF_2}   | = \overline{AB} $$

Pertanto

$$ | \overline{AF_1} - \overline{AF_2} | =  | \overline{BF_2} - \overline{BF_1} | = \overline{AB} $$

Questo dimostra che per qualsiasi punto $ P $ la differenza assoluta delle distanze tra i fuochi è uguale alla distanza tra i vertici dell'iperbole.

$$ | \overline{PF_1} -  \overline{PF_2}   | = \overline{AB} $$

E così via.