Il raggio focale in una conica
Il raggio focale in una conica è il segmento che collega un punto qualsiasi $ P $ di una conica a uno dei suoi fuochi $ F $.
Le coniche sono particolari curve come l'ellisse, la parabola e l'iperbole. Queste curve, dette anche "sezioni coniche", sono ottenute tagliando un cono con un piano in modi diversi.
Per comprendere meglio il raggio focale, devo distinguere tra le diverse coniche:
- Parabola
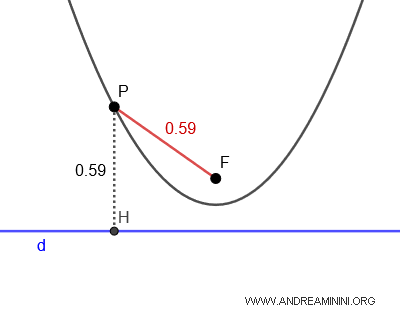
Una parabola ha un solo fuoco $ F $. Quindi, per qualsiasi punto $ P $ della parabola esiste un solo raggio focale $ \overline{PF} $. Inoltre, in una parabola qualsiasi punto $ P $ sulla parabola ha la stessa distanza dal fuoco $ F $ e dalla retta direttrice (d).
- Ellisse
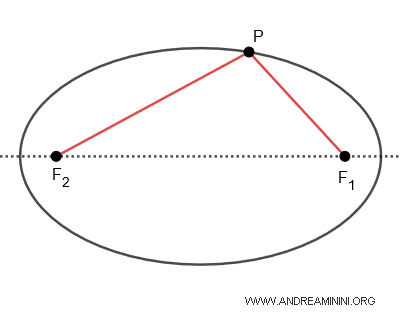
Un'ellisse ha due fuochi $ F_1 $ e $ F_2 $. Quindi ci sono due raggi focali \(PF_1\) e \(PF_2\) per ogni punto $ P $. Inoltre, in una ellisse la somma delle distanze da un qualsiasi punto $ P $ sull'ellisse a ciascuno dei due fuochi è costante $ \overline{PF_1} + \overline{PF_2} = k $.
- Iperbole
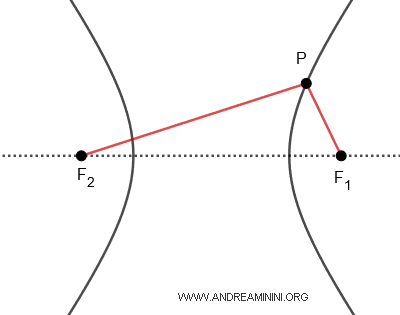
Anche un'iperbole ha due fuochi $ F_1 $ e $ F_2 $. Quindi, se prendo un punto \(P\) sulla curva ci sono due raggi focali $ \overline{PF_1} $ e $ \overline{PF_2} $. Inoltre, la differenza delle distanze da un qualsiasi punto $ P $ sull'iperbole ai due fuochi è costante $ \overline{PF_1} - \overline{PF_2} = k $.
In ogni caso il raggio focale è la distanza tra un punto specifico su una conica (che può essere un'ellisse, una parabola o un'iperbole) e uno dei suoi fuochi.
Il raggio focale è molto utile perché è una misura che lega i punti di una conica ai suoi fuochi e aiuta a definire le proprietà ottiche delle sezioni coniche. Inoltre, ha diverse applicazioni pratiche.
Ad esempio, in un'ellisse, qualsiasi luce o onda sonora che parte da un fuoco verrà riflessa in modo tale da passare per l'altro fuoco. Questo principio è utilizzato in vari dispositivi ottici e acustici. In una parabola, tutte le onde che arrivano parallelamente all'asse di simmetria vengono focalizzate esattamente sul fuoco, il che spiega l'uso delle parabole nelle antenne satellitari e nei fari.
E così via.
