L'accelerazione
In fisica l'accelerazione è la variazione della velocità in un moto. Può essere media o istantanea.
Qual è la differenza?
L'accelerazione media rileva la variazione di velocità di un punto in movimento in un intervallo di tempo (t-t0), mentre l'accelerazione istantanea la rileva in un istante preciso (t).
Quindi, si può dire che l'accelerazione è direttamente proporzionale alla variazione di velocità e inversamente proporzionale al tempo impiegato.
$$ a_m = \frac{Δv}{Δt} = \frac{v_2 - v_1}{t_2 - t_1} $$
L'accelerazione può essere positiva o negativa.
- L'accelerazione positiva
Quando è positiva, l'oggetto sta aumentando la sua velocità, cioè si sta muovendo più velocemente. - L'accelerazione negativa
Quando l'accelerazione è negativa, l'oggetto sta diminuendo la sua velocità, ossia sta rallentando. Questo può anche essere descritto come decelerazione.
L'unità di misura dell'accelerazione nel Sistema Internazionale (SI) è il metro al secondo quadrato (m/s²). Questa unità deriva dalla divisione della velocità (misurata in metri al secondo) per il tempo (misurato in secondi).
Ad esempio, se un oggetto ha un'accelerazione di 3 m/s², questo significa che la sua velocità aumenta di 3 metri al secondo ogni secondo.
Nota. Quando l'accelerazione media di un oggetto, calcolata su qualsiasi intervallo di tempo, è sempre la stessa, si dice che l'oggetto si muove con un moto uniformemente accelerato. In altre parole, l'oggetto sta aumentando la sua velocità a un tasso costante.
L'accelerazione media
In un moto rettilineo l'accelerazione media è il rapporto tra la variazione della velocità in un intervallo di tempo. $$ a_m = \frac{Δv}{Δt} $$
Dove Δt è un intervallo di tempo t-t0.
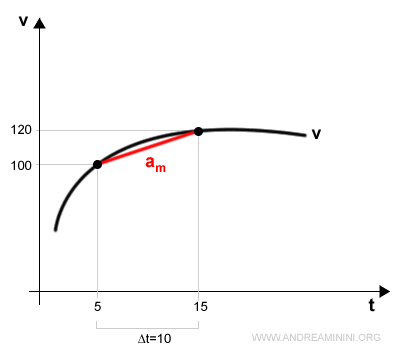
Un esempio pratico
Nell'istante t=0 un treno viaggia alla velocità di 100 km/h.
Dopo 10 secondi, nell'istante t=10, la velocità del treno è di 120 km/h.
Per calcolare l'accelerazione media applico la formula precedente
$$ a_m = \frac{Δv}{Δt} $$
Dove Δv è la variazione di velocità e Δt è la variazione del tempo.
In questo esempio, Δv=20 km/h e Δt=10 secondi.
L'unità di misura corretta per l'accelerazione (a) è metri al secondo quadrato (m/s2).
Pertanto, per essere coerente con le unità SI (Sistema Internazionale), devo convertire la velocità da km/h a m/s prima di fare il calcolo.
La conversione da km/h a m/s si fa dividendo per 3.6 (poiché 1 km/h = 1/3.6 m/s).
$$ Δv=20 km/h=\frac{20}{3.6} \ m/s = 5.55 \ m/s $$
A questo punto posso calcolare correttamente l'accelerazione media:
$$ a_m = \frac{5.55 m/s }{10 s} = 0.55 m/sec^2 $$
L'accelerazione media del treno è stata di 0.55 metri al secondo quadro.
L'accelerazione istantanea
L'accelerazione istantanea è la rapidità di variazione della velocità in un istante t. $$ a = \frac{dv}{dt} $$
E' uguale alla derivata prima della velocità rispetto al tempo.
Nota. Poiché la velocità è la derivata prima della posizione nello spazio x rispetto al tempo, posso anche affermare che l'accelerazione istantanea è la derivata seconda della posizione x nello spazio rispetto al tempo. $$ a = \frac{dv}{dt} = \frac{d^2x}{dt^2} $$
Dal punto di vista grafico l'accelerazione istantanea è il coefficiente angolare della retta tangente al grafico della velocità nell'istante t.
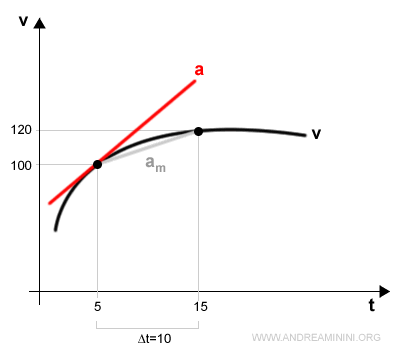
L'accelerazione si ottiene calcolando il limite per Δt→0 del rapporto incrementale
$$ a(t) = \lim_{ \Delta t \rightarrow 0 } \frac{ v(t+Δt) -v(t)}{Δt} = \frac{d \: v}{ d \: t} $$
Il segno algebrico dell'accelerazione istantanea fornisce alcune importanti informazioni
- se a>0 la velocità cresce
- se a=0 la velocità è costante
- se a<0 la velocità si riduce
Conoscendo la funzione di accelerazione posso anche calcolare la velocità del punto in qualsiasi istante.
L'accelerazione vettoriale
Nello spazio la velocità istantanea è un vettore.
$$ \vec{v} = \frac{d \: x}{d \: t} \cdot \hat{u} + \frac{d \: y}{d \: t} \cdot \hat{j} + \frac{d \: z}{d \: t} \cdot \hat{k} $$
$$ \vec{v} = v_x \cdot \hat{u} + v_y \cdot \hat{j} + v_y \cdot \hat{k} $$
Pertanto, anche la variazione della velocità istantanea (ossia l'accelerazione istantanea) è un vettore.
$$ \vec{a} = \frac{d \: v_x}{d \: t} \cdot \hat{u} + \frac{d \: v_y}{d \: t} \cdot \hat{j} + \frac{d \: v_z}{d \: t} \cdot \hat{k} $$
$$ \vec{a} = a_x \cdot \hat{u} + a_y \cdot \hat{j} + a_y \cdot \hat{k} $$
Nota. I versori u,j,k sono costanti in entrambe le precedenti equazioni. Quindi, necessariamente la derivata dvx/dt=ax. Lo stesso vale per dvy/dt=ay e dvz/dt=az.
Posso misurare le variazioni di accelerazione di un punto materiale nel tempo analizzando le variazioni delle singole componenti dell'accelerazione sugli assi x,y,z.
Le componenti dell'accelerazione sono
$$ a_x(t) = \frac{d \: v_x}{d \: t} \cdot \hat{u} $$
$$ a_y(t) = \frac{d \: v_y}{d \: t} \cdot \hat{j} $$
$$ a_z(t) = \frac{d \: v_z}{d \: t} \cdot \hat{k} $$
Poiché la velocità è la derivata prima della posizione, l'accelerazione è la derivata seconda della posizione.
$$ a_x(t) = \frac{d^2 \: x}{d \: t^2} \cdot \hat{u} $$
$$ a_y(t) = \frac{d^2 \: y}{d \: t^2} \cdot \hat{j} $$
$$ a_z(t) = \frac{d^2 \: z}{d \: t^2} \cdot \hat{k} $$
E così via.
