Il vettore posizione
Il vettore posizione è un vettore usato per rappresentare la posizione di un oggetto nello spazio rispetto a un determinato sistema di riferimento.
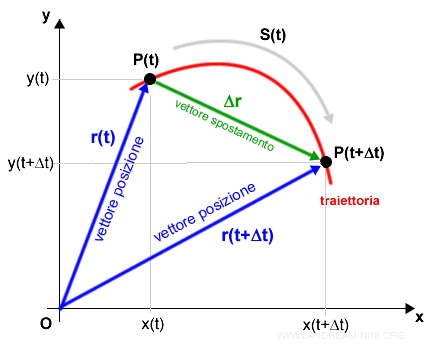
I vettori posizione si indicano con la lettera r oppure r(t) se le coordnate del punto sono in funzione del tempo.
In genere il sistema di riferimento sono gli assi cartesiani x,y,z e il punto di origine O.
Nota. In termini algebrici il sistema di riferimento cartesiano è composto da tre vettori base ortonormali ossia perpendicolari tra loro.
Perché si usa il vettore posizione?
I vettori posizione mi permettono di descrivere la posizione di un punto tramite le sue componenti rispetto ai vettori della base canonica.
Ad esempio, per rappresentare l'oggetto P alle coordinate (x,y,z) posso scrivere il vettore
$$ \vec{r} = x \cdot \vec{i} + y \cdot \vec{j} + z \cdot \vec{k} $$
Dove i vettori i,j,k sono i vettori ortonormali i=(1,0,0) , j=(0,1,0) e k=(0,0,1)
$$ \vec{r} = x \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} + y \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + z \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} $$
I vettori posizione mi permettono di conoscere la distanza di ogni punto rispetto a qualsiasi altro punto che scelgo come origine (O) del sistema di riferimento.
Ad esempio, la distanza del punto P(x,y,z) dall'origine è la lunghezza del vettore posizione, ossia il suo modulo
$$ |r| = \sqrt{x^2 + y^2 + z^2} $$
Nota. L'uso degli assi cartesiani offre diversi vantaggi. Ad esempio, mi permette di utilizzare il teorema di Pitagora e le funzioni trigonometriche semplificando notevolmente il calcolo della distanza dei punti.
Un esempio pratico
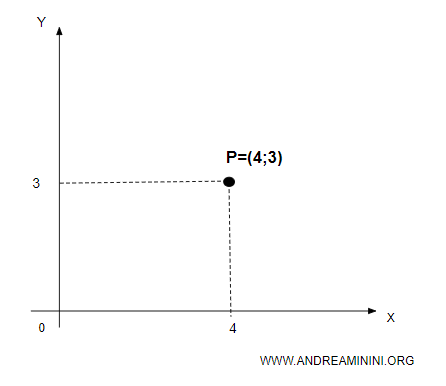
Considero il punto P alle coordinate (4;3) del piano cartesiano
$$ P = (4;3) $$
Il punto si trova alle coordinate cartesiane x=4 e y=3
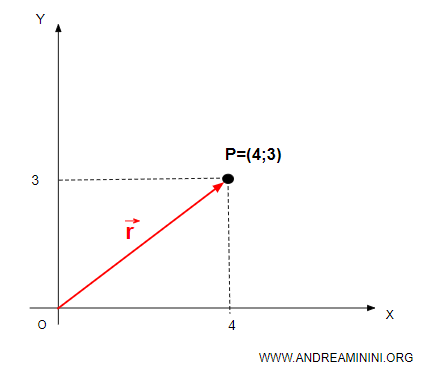
Per rappresentare questo punto utilizzo il vettore posizione r1
$$ \vec{r}_1 = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} $$
Graficamente il vettore posizione è un segmento orientato con la coda nel punto di origine O=(0;0) e la punta nel punto di applicazione P=(4;3).
Le proiezioni del punto P(4;3) sugli assi cartesiani formano un triangolo rettangolo.
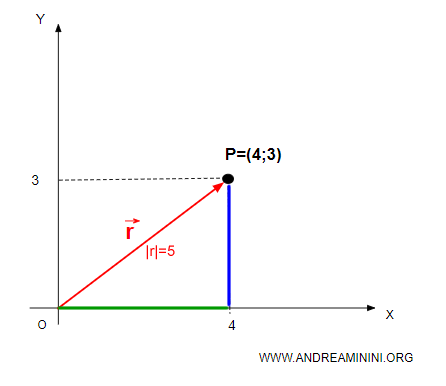
Quindi, per conoscere la distanza dall'origine mi basta calcolare il teorema di Pitagora
$$ \overline{OP} = | \vec{r}_1 | = \sqrt{x^2+y^2} $$
$$ \overline{OP} = | \vec{r}_1 | = \sqrt{4^2+3^2} = \sqrt{16+9} = \sqrt{25} =5 $$
La lunghezza del vettore (o modulo) è |r|=5.
E' la distanza del punto P rispetto all'origine.
E così via.
