L'accelerazione tangenziale e centripeta

L'accelerazione nel moto di un punto materiale su un piano che segue una traiettoria curvilinea è composta da due componenti.

$$ a = a_T + a_N = \frac{dv}{dt} u_T + \frac{v^2}{R} u_N $$

• L'accelerazione tangenziale esprime la variazione del modulo della velocità $$ a_T = \frac{dv}{dt} u_T $$
• L'accelerazione centripeta (o normale) esprime la variazione della direzione della velocità. E' detta "centripeta" perché indica sempre il centro della traiettoria. $$ a_N = \frac{v^2}{R} u_N $$

I due vettori dell'accelerazione a_T e a_N sono tra loro vettori ortogonali ossia formano un angolo di 90°.

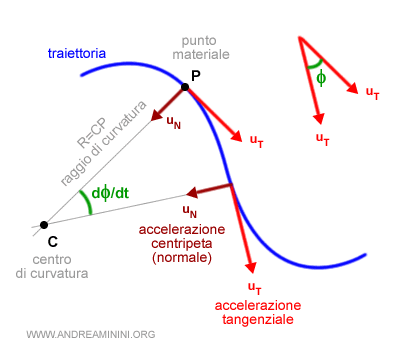
Durante il moto il centro di curvatura C e il raggio di curvatura CP si spostano .

Il raggio di curvatura CP è sempre diretto verso il centro della curva nella parte in cui è concava e può spostarsi da una parte all'altra.

Nota. Il raggio di curvatura non deve essere confuso con il raggio vettore. Sono concetti diversi.

L'accelerazione nel moto curvilineo vario o uniforme

Nel moto curvilineo vario entrambe le accelerazioni a_T e a_N sono diverse da zero.

Con vario si intende che la velocità può variare durante il moto.

Nel moto curvilineo uniforme la velocità non varia. Quindi, in questo caso l'accelerazione tangenziale a_T=0 è nulla.

E nel moto rettilineo? Nel moto rettilineo l'accelerazione è composta soltanto dalla prima componente a_T perché la direzione è costante, mentre a_N=0. Nel caso particolare in cui il moto rettilineo è uniforme (non è vario) anche a_T=0 oltre a_N=0 .

Dai valori dell'accelerazione tangenziale e normale posso dedurre la natura del moto:

• Se a_N≠0 il moto è curvilineo.
• Se a_T≠0 il moto è vario.
• Se a_T=0 il moto è uniforme

Ecco una tabella riassuntiva

Dimostrazione

L'accelerazione è la derivata della velocità.

$$ a = \frac{dv}{dt} $$

Considerando la direzione della velocità

$$ a = \frac{dv \cdot u_T}{dt} $$

Svolgo la derivata del prodotto

$$ a = \frac{dv}{dt} \cdot u_T + v \cdot \frac{d \: u_T}{dt} $$

Sapendo che la derivata di un versore è un vettore ortogonale, la derivata del versore tangente u_T è la velocità angolare ω=dΦ/dt $$ \frac{d \: u_T}{dt} = \frac{d \: Φ}{dt} \cdot u_N $$

$$ a = \frac{dv}{dt} \cdot u_T + v \cdot ( \frac{d \: Φ}{dt} \cdot u_N ) $$

Sapendo che un'angolo in radianti (Φ) è pari al rapporto tra l'arco (s) e il raggio (R). $$ \frac{d \: Φ}{dt} = \frac{d ( \frac{s}{R} ) }{dt} $$ dove R=CP è il raggio di curvatura ed è costante, quindi esce dalla derivata $$ \frac{dΦ}{dt} = \frac{d ( \frac{s}{R} ) }{dt} = \frac{1}{R} \cdot \frac{ds}{ dt } $$ La derivata dello spazio percorso rispetto al tempo è la velocità v=ds/dt. $$ \frac{dΦ}{dt} = \frac{d ( \frac{s}{R} ) }{dt} = \frac{1}{R} \cdot \frac{ds}{ dt } = \frac{1}{R} \cdot v = \frac{v}{R} $$ Pertanto, posso sostituire $$ \frac{dΦ}{dt} = \frac{v}{R} $$

$$ a = \frac{dv}{dt} \cdot u_T + v \cdot ( ( \frac{v}{R} ) \cdot u_N ) $$

$$ a = \frac{dv}{dt} \cdot u_T + \frac{v^2}{R} \cdot u_N $$

I due addendi sono l'accelerazione tangenziale e l'accelerazione normale

$$ a_T = \frac{dv}{dt} \cdot u_T $$

$$ a_N = \frac{v^2}{R} \cdot u_N $$

Pertanto, l'accelerazione è la somma delle due accelerazioni

$$ a = a_T + a_N $$

Essendo queste ultime sono grandezze vettoriali, si tratta di una somma tra vettori.

$$ \vec{a} = \vec{a_T} + \vec{a_N} $$

Quindi, il modulo dell'accelerazione |a| è

$$ |a| = \sqrt{a_T^2 + a_N^2} $$

$$ |a| = \sqrt{ ( \frac{dv}{dt} )^2 + ( \frac{v^2}{R} )^2 } $$

E così via.