La velocitÓ radiale e trasversa
La rappresentazione polare della velocità
La velocità può essere rappresentata tramite le coordinate polari.
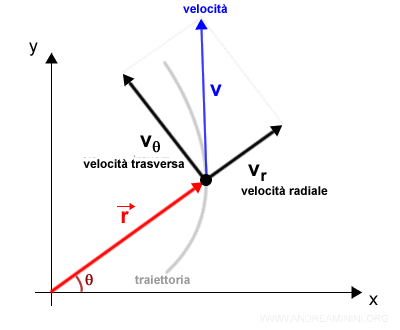
E' suddivisa in due componenti:
- La velocità radiale
Un vettore nella direzione del raggio vettore.
$$ v_r = \frac{ d \: r }{d \: t} \cdot \hat{u_r} $$ - La velocità trasversa
Un vettore ortogonale al raggio vettore
$$ v_θ = r \cdot \frac{d \: u_r} {d \: t} = r \cdot \frac{d \: θ} {d \: t} \cdot u_θ $$
La formula della velocità polare è
$$ \vec{v} = \vec{v_r} + \vec{v_θ} $$
Nota. Indipendentemente dalla rappresentazione la velocità è sempre tangente alla traiettoria del punto materiale in movimento.
Come calcolare la velocità
La velocità radiale vr e la velocità trasversa vθ sono i cateti di un triangolo composto con il modulo della velocità.
Quindi, per calcolare la velocità posso usare il teorema di Pitagora.
$$ v = \sqrt{v_θ^2 + v_r^2} $$
La dimostrazione
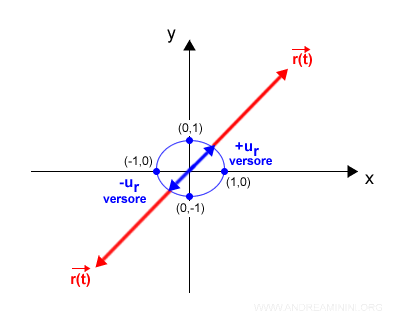
Prendo in considerazione il raggio vettore r(t)
$$ \vec{r}(t) = r \cdot u_r $$
Dove ur è il versore del raggio vettore e indica il verso del vettore lungo la direzione.
La variabile r è invece il modulo ossia la lunghezza del vettore
Esempio. Se il modulo del raggio vettore |r|=3 e il versore ur=(1/√2,-1/√2) il raggio vettore si trova nel quarto quadrante.
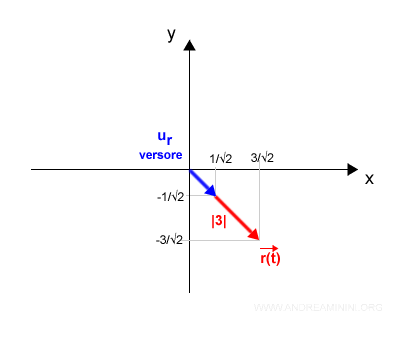
perché r(t) = ur·|r| $$ r(t) = u_r \cdot |r| $$ $$ r(t) = \begin{pmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{pmatrix} \cdot |3| $$ $$ r(t) = \begin{pmatrix} \frac{|3|}{\sqrt{2}} \\ -\frac{|3|}{\sqrt{2}} \end{pmatrix} $$ Sono le coordinate cartesiane (x,y) del vettore geometrico sul piano.
Sapendo che la velocità v è uguale alla derivata del raggio vettore r(t) rispetto al tempo
$$ \vec{v} = \frac{d \: \vec{r}(t) }{d \:t} = \frac{d \: \hat{u_r} \cdot r }{d \:t} $$
Per la legge della derivata del prodotto ottengo
$$ \frac{d \: \vec{r}(t) }{d \:t} = \hat{u_r} \cdot \frac{ d \: r }{d \: t} + r \cdot \frac{d \: \hat{u}_r} {d \: t} $$
La prima componente è la velocità radiale
$$ \frac{d \: \vec{r}(t) }{d \:t} = v_r + r \cdot \frac{d \: \hat{u}_r } {d \: t} $$
Nota. La formula della velocità radiale è $$ v_r = \hat{u_r} \cdot \frac{ d \: r }{d \: t} $$
La seconda componente è la velocità trasversa
$$ \frac{d \: \vec{r}(t) }{d \:t} = v_r + v_θ $$
Nota. La formula della velocità trasversa è $$ v_θ = r \cdot \frac{d \: u_r} {d \: t} = r \cdot \frac{d \: θ} {d \: t} \cdot u_θ $$
E così via
