Come trovare un punto equidistante a due punti

Dati due punti A e B distinti del piano, devo individuare un punto C equidistante sia da A che da B.

Traccio una prima circonferenza con centro A e raggio AB.

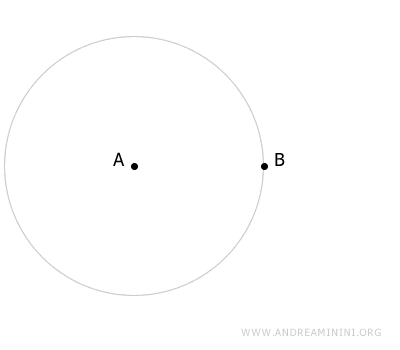
Poi traccio una seconda circonferenza mantenendo la stessa apertura del compasso, questa volta con centro B.

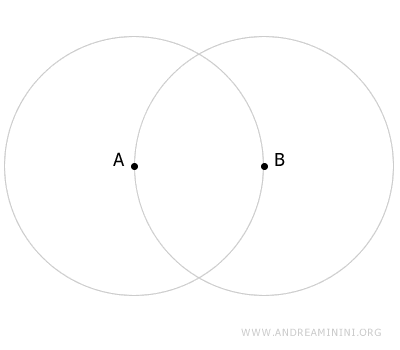
Le due circonferenze si intersecano in due punti distinti C e C'.

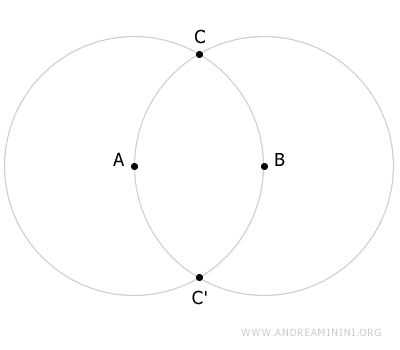
I punti C e C' sono equidistanti sia dal punto A che dal punto B.

Dimostrazione. I punti C e B appartengono alla stessa circonferenza con centro A. Pertanto, i segmenti AB e AC sono congruenti. $$ AB \cong AC $$ D'altra parte, i punti C e A appartegono alla stessa circonferenza con centro B. Quindi, i segmenti AB e CB sono tra loro congruenti. $$ AB \cong BC $$ Se AB≅AC e AB≅BC, allora per la proprietà transitiva anche i segmenti AC e BC sono congruenti tra loro. $$ AC \cong BC $$ Pertanto, i punti A, B e C si trovano alla stessa distanza. La stessa dimostrazione posso ripeterla sostituendo C con C'.

E così via.