Come trovare il punto medio di un segmento 

Per trovare il punto medio di un segmento AB, punto il compasso sull'estremo A e apro il compasso con un'apertura a piacere, purché sia maggiore della metà del segmento, e traccio un arco.

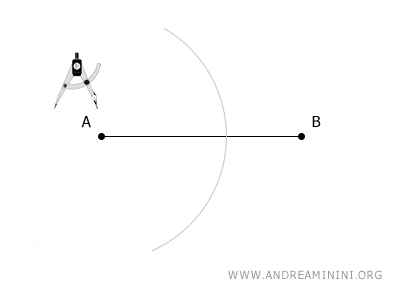
Ora punto il compasso sull'altro estremo B del segmento e traccio un secondo arco con la stessa apertura del compasso.

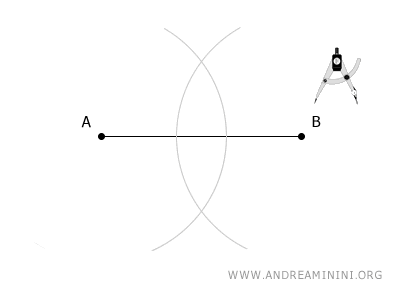
I due archi si intersecano nei punti C e D del piano.

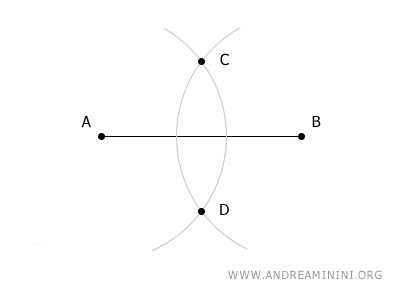
Il segmento che congiunge i punti C e D interseca il segmento AB nel suo punto medio M.

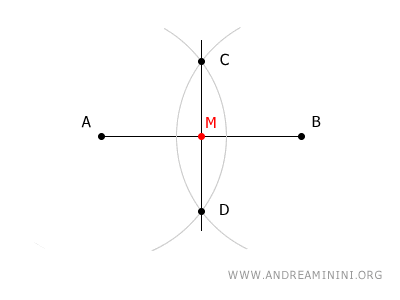
In questo modo ho trovato il punto medio del segmento.

Dimostrazione. Per costruzione i segmenti $ AC \cong BC \cong AD \cong BD $ sono congruenti. Quindi i triangoli $ ACD \cong BCD $ sono congruenti per il terzo criterio di congruenza dei triangoli, perché hanno tutti i lati congruenti nello stesso ordine.

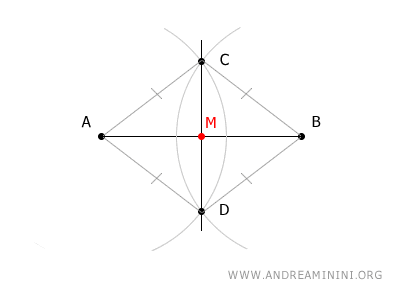
Pertanto i triangoli ACD e BCD hanno gli angoli ordinatamente congruenti. In particolar modo, mi interessa sapere che sono congruenti gli angoli $ A \hat{C} D \cong B \hat{C} D  $ perché da questo deduco che il segmento $ CM $ è la bisettrice dell'angolo $ A \hat{C}B $ del triangolo $ ABC $ che è anche un triangolo isoscele, perché ha due lati congruenti $ AC \cong BC $.

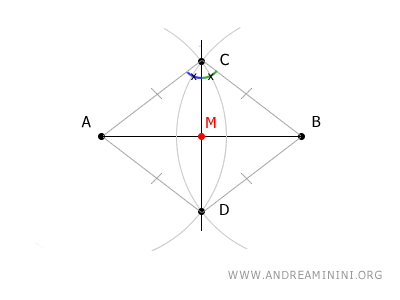
In un triangolo isoscele la bisettrice è anche la mediana dello stesso vertice. Poiché la mediana cade nel punto medio del lato $ AB $ del triangolo ABC, questo dimostra che $ M $ è il punto medio del segmento AB.

E così via.