Come trovare la bisettrice di un angolo
Considero un angolo α qualsiasi di cui devo trovare la bisettrice, ossia la semiretta che divide l'ampiezza dell'angolo a metà.
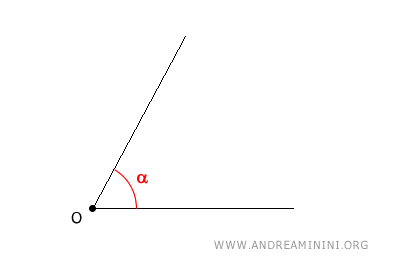
Centro il compasso sul vertice O dell'angolo e traccio un arco con un'apertura a piacere, facendo in modo che l'arco intersechi i due lati dell'angolo.
In questo modo trovo due punti A e B sui lati dell'angolo, equidistanti dal vertice.
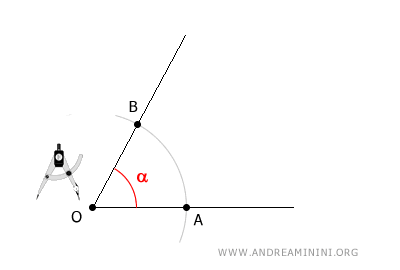
A questo punto centro il compasso sul punto A e con un'apertura "r" a piacere, anche diversa da quella precedente, traccio un arco.
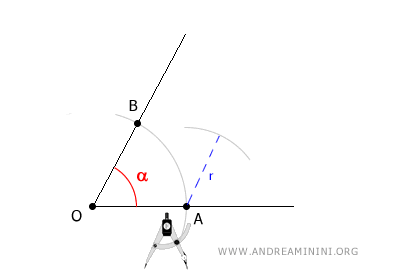
Poi, mantenendo la stessa apertura "r", centro il compasso sul punto B e traccio un altro arco che interseca il precedente.
L'intersezione tra i due archi individua un punto C.
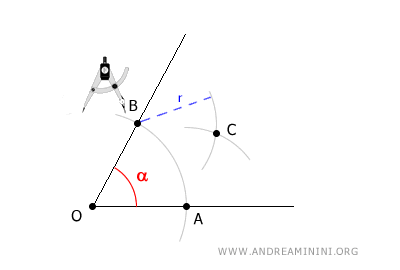
Traccio una semiretta passante per il vertice O e per il punto C che ho appena trovato.
La semiretta OC passante per i punti O e C è la bisettrice dell'angolo.
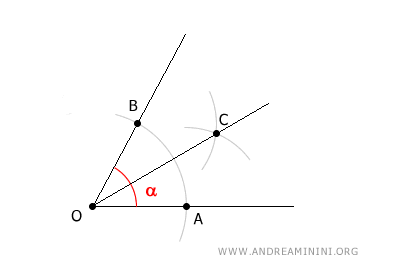
In questo modo ho diviso l'angolo α in due parti uguali.
Dimostrazione. Vediamo come si può dimostrare di aver trovato effettivamente la bisettrice dell'angolo. Considero i triangoli OAC e OBC.
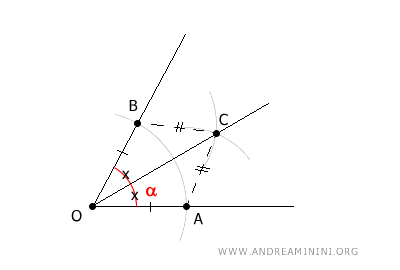
Questi due triangoli hanno un lato coincidente (OC) e gli altri due lati (OA=OB) e (AC=BC) per costruzione. Quindi, per il terzo criterio di congruenza dei triangoli sono triangoli congruenti $$ OAC \cong OBC $$ Essendo triangoli congruenti, hanno gli angoli congruenti nello stesso ordine. Quindi anche gli angoli $ A \hat{O} C \cong B \hat{O} C $ sono congruenti e questo dimostra che il segmento $ OC $ è la bisettrice che taglia a metà l'angolo $ A \hat{O} B $.
E così via.
