Come trovare l'ortocentro in un triangolo
Per trovare l'ortocentro in un triangolo devo tracciare le tre altezze per ciascun lato.
L'altezza di un triangolo è il segmento perpendicolare a un lato (o al suo prolungamento) che passa per il vertice opposto.
Considero un triangolo ABC qualsiasi (ottusangolo, acutangolo o rettangolo). In questo caso è un triangolo scaleno acutangolo.
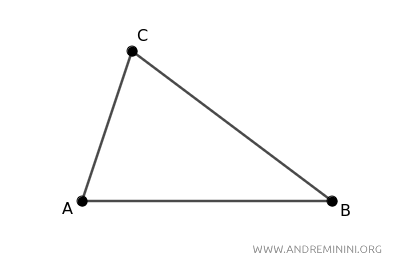
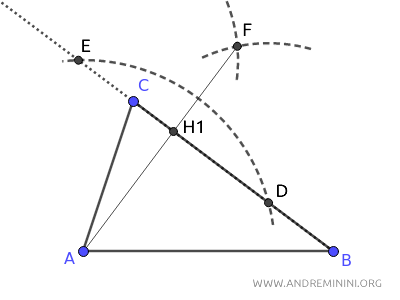
Punto il compasso sul vertice A e traccio un arco che interseca in due punti distinti il lato opposto BC (o il suo prolungamento) in due punti D e E.
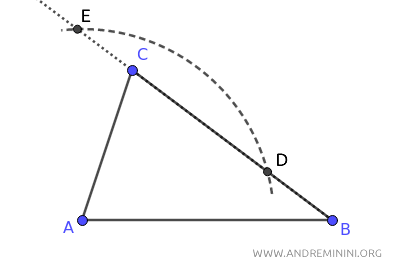
Poi con un'apertura del compasso a piacere, anche diversa dalla precedente purché sia maggiore della metà del segmento DE, punto il compasso sul punto D traccio un arco.
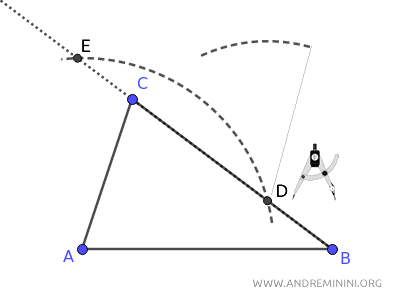
Mantenendo la stessa apertura, punto il compasso sul punto E e traccio un altro arco che interseca il precedente nel punto F.
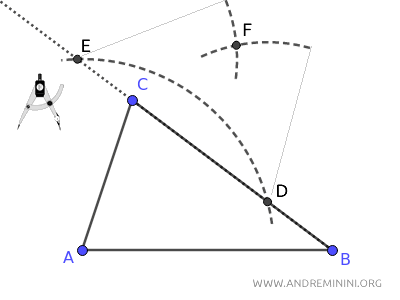
Infine disegno un segmento tra il vertice A e il punto F che interseca il lato BC del triangolo nel punto H1.
Il segmento AH1 è l'altezza del triangolo rispetto al lato BC.
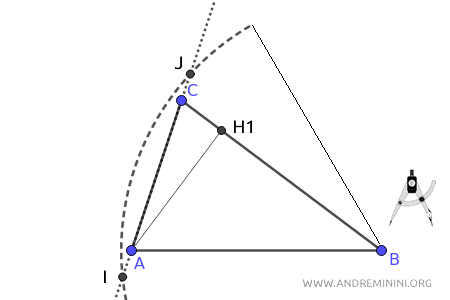
Ora punto il compasso su B e con un'apertura a piacere del compasso traccio un arco che interseca in due punti distiniti I e J il lato opposto AC (o un suo prolungamento).
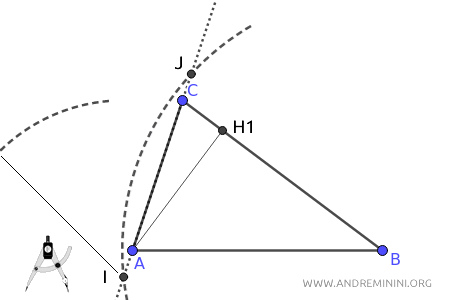
Centro il compasso sul punto I e con un'apertura a piacere, purché maggiore della metà del segmento IJ, traccio un arco.
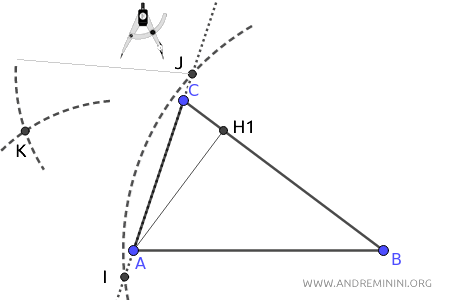
Ora centro il compasso sul punto J con la stessa apertura e traccio un secondo arco che interseca il precedente nel punto K.
Traccio un segmento tra il vertice B e il punto K che interseca il lato AC del triangolo nel punto H2.
Il segmento BH2 è l'altezza del triangolo rispetto al lato AC.
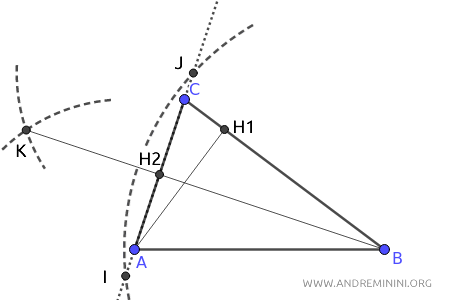
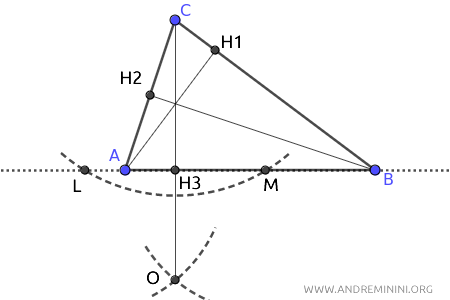
Infine, punto il compasso sul vertice C e traccio un arco che interseca il segmento AB (o il suo prolungamento) in due punti distinti L e M.
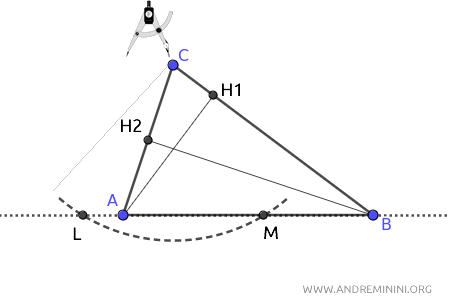
Poi punto il compasso su L e con un'apertura a piacere (purché maggiore della metà del segmento LM) traccio un arco.
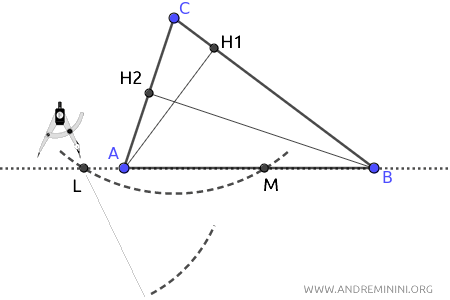
Mantenendo la stessa apertura, centro il compasso su M e traccio un secondo arco che interseca il precedente nel punto O.
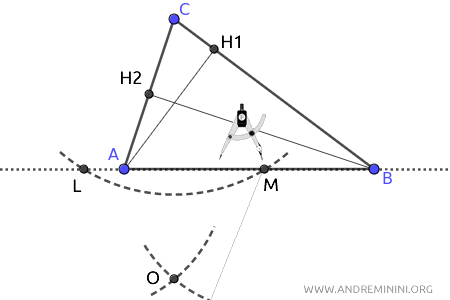
Traccio un segmento tra il vertice C e il punto O che interseca il lato AB nel punto H3.
Il segmento CH3 è l'altezza del triagolo rispetto al lato AB.
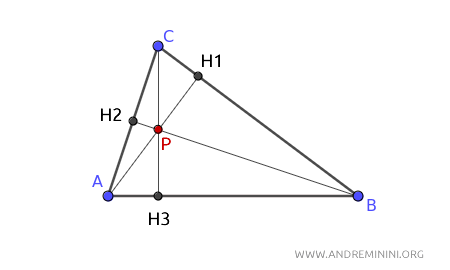
Le tre altezze del triangolo si intersecano nel punto P che è l'ortocentro del triangolo.
E così via.
