Serie armonica
Questa serie è detta serie armonica $$ \sum_{k=1}^{\infty} \frac{1}{k} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + ... $$
La serie armonica è la somma dei reciproci dei numeri naturali.
Si tratta di una serie divergente anche se la divergenza non è subito evidente.
Un esempio pratico
Ecco una rappresentazione grafica delle somme parziali della serie armonica per k che tende a infinito.
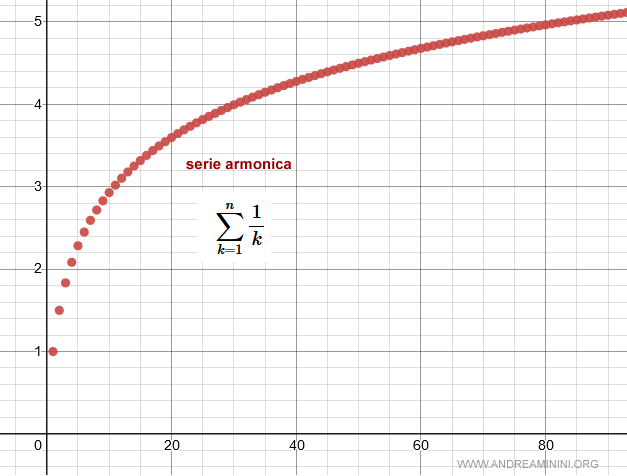
Il carattere della serie armonica
La serie armonica diverge a infinito per k→∞.
La successione dei termini della serie armonica tende a zero k→∞.
Quindi, rispetta la condizione necessaria della convergenza di una serie.
$$ \lim_{k \rightarrow \infty} \frac{1}{k} = 0 $$
Nota. Questa condizione però è soltanto necessaria alla convergenza della serie. Non è una condizione sufficiente. E' opportuno non dimenticarlo.
Tuttavia, la serie armonica è una serie divergente.
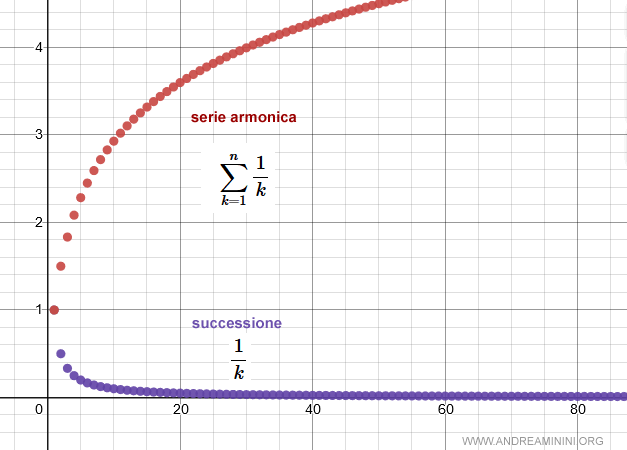
La dimostrazione
Per dimostrare la divergenza della serie armonica, prendo come riferimento la successione ak
$$ a_k = (1 + \frac{1}{k} )^k $$
Si tratta di una successione crescente per k→∞.
Il limite della successione per k→∞ è anche un limite notevole, molto conosciuto, che tende al numero di Nepero (e).
$$ \lim_{k \rightarrow \infty} (1 + \frac{1}{k} )^k = e $$
Pertanto, la successione è crescente e convergente al numero di Nepero (e).
Posso affermare che
$$ e \ge (1 + \frac{1}{k} )^k \:\:\:\: \forall k \in N $$
Applico il logaritmo a entrambi i membri.
Ottengo una disequazione equivalente.
$$ \log e \ge \log (1 + \frac{1}{k} )^k $$
Sapendo che il logaritmo dell'esponenziale è 1.
$$ 1 \ge \log (1 + \frac{1}{k} )^k $$
Applico la regola dell'esponente di un logaritmo.
$$ 1 \ge k \cdot \log (1 + \frac{1}{k} ) $$
Con un semplice passaggio algebrico ottengo
$$ \frac{1}{k} \ge \log (1 + \frac{1}{k} ) $$
$$ \frac{1}{k} \ge \log ( \frac{k+1}{k} ) $$
Poi applico la regola del rapporto di un logaritmo.
$$ \frac{1}{k} \ge \log ( k+1 ) - \log k $$
Quest'ultima disequazione mi fa capire che la successione 1/k è sempre maggiore uguale alla successione log(k+1)-log k.
Calcolo la sommatoria per k→n a entrambi i membri della disequazione
$$ \sum_{k=1}^{n} \frac{1}{k} \ge \sum_{k=1}^{n} \log ( k+1 ) - \log k $$
Nel membro di sinistra c'è la serie armonica.
Quindi, la serie armonica è maggiore uguale alla serie log(k+1)-log k.
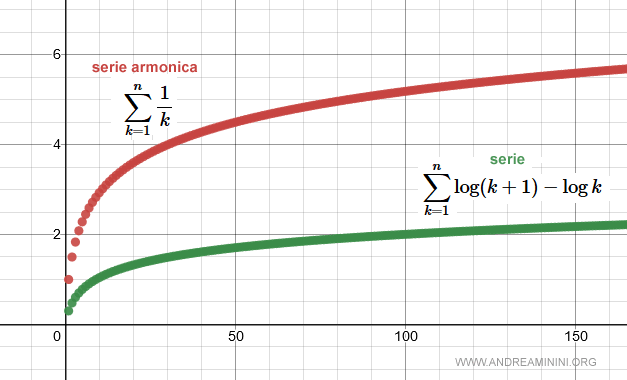
Questo mi permette di studiare il carattere della serie armonica per confronto con la serie log(k+1)-log(k).
La serie log(k+1)-log(k) è uguale a log(n+1).
$$ \sum_{k=1}^{n} \frac{1}{k} \ge log(n+1) $$
Spiegazione. La serie $$ \sum_{k=1}^{n} \log ( k+1 ) - \log k $$ si sviluppa in questo modo $$ \sum_{k=1}^{n} \log ( k+1 ) - \log k = (\log 2 - \log 1) + (\log 3 - \log 2) + (\log 4 - \log 3) + ... + ( \log n+1 - \log n ) $$ Quindi, il primo minuendo è sempre annullato dal sottraendo del fattore successivo.
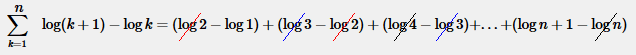
Pertanto la serie è uguale a $$ \sum_{k=1}^{n} \log ( k+1 ) - \log k = - \log 1 + \log n+1 $$ ossia $$ \sum_{k=1}^{n} \log ( k+1 ) - \log k = \log n+1 - \log 1 $$ Poiché il logaritmo di 1 è zero, il risultato è $$ \sum_{k=1}^{n} \log ( k+1 ) - \log k = \log n+1 $$.
A questo punto, studio il carattere della successione log(n+1) sapendo che è sempre inferiore alla serie armonica per qualsiasi k.
Calcolo il limite per n→∞ in entrambi i membri della disequazione.
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^{n} \frac{1}{k} \ge \lim_{n \rightarrow \infty} log(n+1) $$
Poiché il limite del logaritmo n+1 è infinito.
$$ \lim_{n \rightarrow \infty} log(n+1) = \infty $$
Posso riscrivere la disequazione precedente in questo modo
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^{n} \frac{1}{k} \ge \infty $$
Quindi anche il limite della serie armonica per n→∞ è infinito.
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^{n} \frac{1}{k} = \infty $$
Questo dimostra la divergenza della serie armonica per n→∞.
Dimostrazione alternativa
Una dimostrazione alternativa del carattere della serie armonica deriva da questa semplice proposizione dei numeri positivi.
$$ \frac{1}{x} \le \frac{1}{k} \:\:\:\: \forall x \ge k $$
Calcolo l'integrale definito dx con estremi da k a k+1 a entrambi i membri della disequazione
$$ \int_{k}^{k+1} \frac{1}{x} \: dx \le \int_{k}^{k+1} \frac{1}{k} \: dx $$
Sposto 1/k al di fuori dell'integrale
$$ \int_{k}^{k+1} \frac{1}{x} \: dx \le \frac{1}{k} \cdot \int_{k}^{k+1} \: dx $$
Calcolo l'integrale al secondo membro con la formula fondamentale dell'integrazione.
$$ \int_{k}^{k+1} \frac{1}{x} \: dx \le \frac{1}{k} \cdot [ (k+1)-k ] $$
$$ \int_{k}^{k+1} \frac{1}{x} \: dx \le \frac{1}{k} \cdot 1 $$
$$ \int_{k}^{k+1} \frac{1}{x} \: dx \le \frac{1}{k} $$
Calcolo la sommatoria Σ per k da 1 a n a entrambi i membri della disequazione
$$ \sum_{k=1}^n \int_{k}^{k+1} \frac{1}{x} \: dx \le \sum_{k=1}^n \frac{1}{k} $$
Il secondo membro della disequazione è la serie armonica
Per la proprietà additiva degli integrali posso riscrivere il primo membro della disequazione in questo modo
$$ \int_{1}^{n+1} \frac{1}{x} \: dx \le \sum_{k=1}^n \frac{1}{k} $$
Spiegazione. Sviluppando la serie del primo membro. $$ \sum_{k=1}^n \int_{k}^{k+1} \frac{1}{x} \: dx = \int_{1}^{2} \frac{1}{x} \: dx + \int_{2}^{3} \frac{1}{x} \: dx + \int_{3}^{4} \frac{1}{x} \: dx + ... + \int_{n}^{n+1} \frac{1}{x} \: dx $$ E' subito evidente che si tratta della somma delle superfici sotto il grafico della funzione 1/x da 1 a n+1. Pertanto, posso scrivere in modo equivalente. $$ \sum_{k=1}^n \int_{k}^{k+1} \frac{1}{x} \: dx = \int_{1}^{n+1} \frac{1}{x} \: dx $$
Calcolo l'integrale al primo membro con la formula fondamentale dell'integrazione.
$$ \log(n+1) - log(1) \le \sum_{k=1}^n \frac{1}{k} $$
Il logaritmo log(1)=0 è uguale a zero
$$ \log(n+1) \le \sum_{k=1}^n \frac{1}{k} $$
Ora calcolo il limite per n→∞ a entrambi i membri
$$ \lim_{n \rightarrow \infty} \log(n+1) \le \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{k} $$
Il limite al membro di destra diverge a infinito
$$ \infty \le \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{k} $$
Quindi il limite della serie armonica è maggiore di infinito.
Secondo il teorema del confronto delle serie anche il limite della serie armonica diverge a infinito.
Ho dimostrato la divergenza della serie armonica.
E così via.
