Il teorema del confronto delle serie
Date due successioni an e bn, tali che $$ 0 \le a_n \le b_n \:\:\: \forall n $$ se la serie bn è convergente, allora anche la serie an è convergente $$ \sum_{k=1}^{\infty} b_k < +\infty \Rightarrow \sum_{k=1}^{\infty} a_k < + \infty $$ se la serie an è divergente, allora anche la serie bn è divergente $$ \sum_{k=1}^{\infty} a_k = +\infty \Rightarrow \sum_{k=1}^{\infty} b_k = + \infty $$
Si applica se le serie sono serie a termini non negativi.
A cosa serve?
Il criterio del confronto mi consente di determinare il carattere di una serie a termini non negativi, confrontandola con un'altra serie di cui conosco il carattere.
E' uno dei criteri di convergenza delle serie numeriche.
Come stabilire la diseguaglianza tra le successioni? E' sufficiente assumere la relazione di diseguaglianza tra le successioni an≤bn per un valore n molto grande.
Un esempio pratico
Esempio 1
Ho le successioni
$$ a_n = \frac{n}{n+1} $$
$$ b_n = \frac{n+2}{n} $$
Preso un n molto grande, tra le successioni vale la relazione diseguaglianza
$$ a_n \le b_n $$
Esempio. Preso n=100 le successioni assumono i seguenti valore: $$ a_{100} = \frac{100}{100+1} = \frac{100}{101} $$ $$ b_{100} = \frac{100+2}{100} = \frac{102}{100} $$
La relazione di diseguaglianza vale anche per le rispettive serie, perché applicando la sommatoria da 1 a n vale la relazione seguente:
$$ \sum_{k=1}^n a_k \le \sum_{k=1}^n b_k $$
Le due serie sono serie a termini non negativi. Quindi posso applicare il teorema del confronto delle serie.
Calcolo il limite per n che tende infinito a entrambe le serie
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^n a_k \le \lim_{n \rightarrow \infty} \sum_{k=1}^n b_k $$
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{n}{n+1} \le \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{n+2}{n} $$
Sapendo che la serie ridotta n-esima an diverge a +∞
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{n}{n+1} = +∞$$
Nota. La serie ridotta an è divergente perché la successione an per n che tende a infinito non tende a zero bensì a 1. Pertanto, non rispetta la condizione necessaria per la convergenza della serie. $$ \lim_{n \rightarrow \infty} \frac{n}{n+1} = 1 \ne 0 $$ Poiché è una serie a termini non negativi, la serie ammette sempre un limite finito o infinito. Non essendo convergente, per esclusione è divergente.
Per la relazione di diseguaglianza anche la serie bn deve divergere a +∞.
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{n}{n+1} \le \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{n+2}{n} $$
$$ +∞ \le \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{n+2}{n} $$
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{n+2}{n} \ge + \infty $$
Pertanto, anche la serie bn è divergente.
Esempio 2
Ho due successioni
$$ a_n = \frac{1}{n^3+1} $$
$$ b_n = \frac{1}{n(n+1)} $$
Preso un n molto grande, tra le successioni vale la relazione diseguaglianza
$$ a_n \le b_n $$
Esempio. Preso n=100 le successioni assumono i seguenti valore: $$ a_{100} = \frac{1}{100^3+1} = \frac{1}{100001} $$ $$ b_{100} = \frac{1}{100·101} = \frac{1}{10100} $$
La relazione di diseguaglianza vale anche per le rispettive serie ridotte n-esime.
$$ \sum_{k=1}^n a_k \le \sum_{k=1}^n b_k $$
$$ \sum_{k=1}^n \frac{1}{n^3+1} \le \sum_{k=1}^n \frac{1}{n(n+1)} $$
Calcolo il limite per n che tende infinito a entrambe le serie
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{n^3+1} \le \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{n(n+1)} $$
La serie bn è la serie di Mengoli.
Sapendo che la serie di Mengoli (bn) converge a 1
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{n(n+1)} =1 $$
per la relazione di diseguaglianza an≤bn anche la serie an deve convergere a 1
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{n^3+1} \le \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{n(n+1)} $$
$$ \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{n^3+1} \le 1 $$
Quindi, anche la serie an (blu) è una serie convergente.
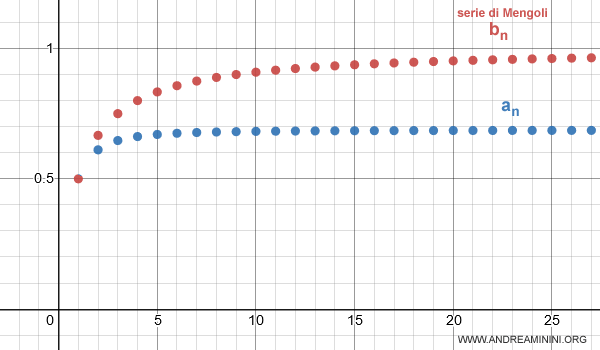
Nota. La serie bn converge a 1 perché è una serie a termini non negativi. Quindi non può assumere valori inferiori allo zero. $$ 0 \le \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{n^3+1} \le 1 $$
Dimostrazione e spiegazione
Date due successioni an e bk, considero le rispettive serie ridotte n-esime un e tn.
$$ u_n = \sum_{k=1}^n a_k $$
$$ t_n = \sum_{k=1}^n b_k $$
Per ipotesi, le due serie sono serie a termini non negativi.
$$ 0 < a_k \le b_k $$
Essendo serie a termini non negativi, le due serie ridotte ammettono un limite finito o infinito per n che tende a infinito.
$$ \lim_{n \rightarrow \infty } u_n = \{ l , \infty \} $$
$$ \lim_{n \rightarrow \infty } t_n = \{ l , \infty \} $$
Inoltre, essendo la successione ak≤bk anche la serie ridotta un è inferiore o uguale alla serie tn per ogni n
$$ u_n \le t_n \:\:\: \forall n $$
Pertanto
$$ \lim_{n \rightarrow \infty } u_n \le \lim_{n \rightarrow \infty } t_n $$
Se il limite della serie ridotta tn è un numero finito, ossia è inferiore a +infinito, la serie tn è convergente.
$$ \le \lim_{n \rightarrow \infty } t_n = l < + \infty $$
Per la relazione di diseguaglianza anche la serie un deve essere convergente.
$$ \lim_{n \rightarrow \infty } u_n \le \lim_{n \rightarrow \infty } t_n = l < + \infty $$
$$ \lim_{n \rightarrow \infty } u_n \le l < + \infty $$
$$ \lim_{n \rightarrow \infty } u_n < + \infty $$
Viceversa, se il limite della serie ridotta un è infinito, la serie un è divergente
$$ \lim_{n \rightarrow \infty } u_n = \infty $$
Per la relazione di diseguaglianza anche la serie tn deve essere divergente.
$$ \lim_{n \rightarrow \infty } u_n = + \infty \le \lim_{n \rightarrow \infty } t_n $$
$$ + \infty \le \lim_{n \rightarrow \infty } t_n $$
$$ \lim_{n \rightarrow \infty } t_n \ge + \infty $$
Il teorema del confronto delle serie a termini non negativi è dimostrato.
E così via.
