La sommatoria
Una sommatoria è una funzione definita che somma n termini di una successione. Si indica con la notazione sigma. $$ \sum_{i=k}^{n} a_i = a_k + a_{k+1}+a_{k+2}+ ... + a_n $$
La variabile i è detta indice della sommatoria.
Al posto della variabile i posso usare qualsiasi altra lettera ( es. i, j, k, t, ecc. ).
Nota. La stessa sommatoria posso scriverla in molti modi equivalenti. Ad esempio, queste due sommatorie sono identiche $$ \sum_{i=1}^{n} a_i = \sum_{i=0}^{n-1} a_{i+1} $$
Esempio di sommatoria
Ho la successione {ai}=2i
$$ \{a_i\} = 2, 4, 6, 8, 10, 12, ... $$
La sommatoria dei primi quattro termini della successione è
$$ \sum_{i=1}^{4 } 2 \cdot i = 2+4+6+8 = 20 $$
Il valore a destra (20) è la somma dei primi quattro termini della successione.
Le proprietà delle sommatorie
Le sommatorie soddisfano le seguenti proprietà:
$$ \sum_{k=1}^{n} c \cdot a_k = c \cdot \sum_{k=1}^{n} a_k $$
$$ \sum_{k=1}^{n} ( a_k + b_k ) = \sum_{k=1}^{n} a_k + \sum_{k=1}^{n} b_k $$
$$ \sum_{k=1}^{n} ( a_k - b_k ) = \sum_{k=1}^{n} a_k - \sum_{k=1}^{n} b_k $$
$$ \sum_{k=1}^{n} a_k = \sum_{k=1}^{m} a_k + \sum_{k=m+1}^{n} a_k $$
$$ Se \:\: A⋂B = Ø \:\:,\:\: \sum_{k \in A} a_k + \sum_{k \in B} a_k = \sum_{k \in A∪B} a_k $$
Le sommatorie e le matrici
La sommatoria posso usarla per leggere gli elementi in una riga o in una colonna di una matrice mxn.
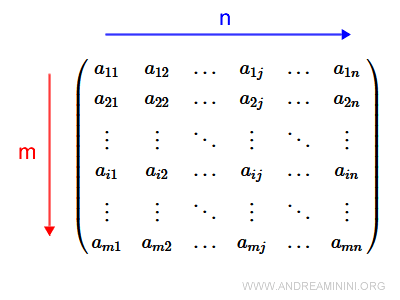
In questo caso, ogni termine della sommatoria è composto da due indici:
- i = numero riga
- j = numero colonna
L'indice della sommatoria scorre gli elementi nella riga (i) oppure nella colonna (j)
$$ \sum_{i=1}^{m} a_{i,j} $$
$$ \sum_{j=1}^{n} a_{i,j} $$
Per leggere tutti gli elementi di una matrice uso la doppia sommatoria.
$$ \sum_{i=1}^{m} \sum_{j=1}^{n} a_{i,j} $$
La sommatoria più interna legge gli elementi delle colonne j da 1 a n nella riga i-esima.
La sommatoria più esterna scorre le righe i da 1 a m.

In questo modo la doppia sommatoria legge tutti gli elementi della matrice riga dopo riga.
Nota. La lettura degli elementi può anche avvenire per colonne. Basta invertire la disposizione delle due sommatorie. $$ \sum_{j=1}^{n} \sum_{i=1}^{m} a_{i,j} $$ In quest'altro modo la lettura è colonna dopo colonna.

E così via.
