Serie di Taylor
Data una funzione f(x) e un intervallo [x0-δ,x0+δ] intorno a un punto x0 con δ>0 in cui la funzione è infinitamente derivabile, la funzione è sviluppabile in serie di Taylor se per ogni x∈[x0-δ,x0+δ] la seguente serie è convergente $$ \sum_{k=0}^{\infty} \frac{f^{(k)}(x_0)}{k!} (x-x_0)^k $$ e la somma è uguale a f(x) $$ f(x) = \sum_{k=0}^{\infty} \frac{f^{(k)}(x_0)}{k!} (x-x_0)^k $$ per ogni x dell'intorno [x0-δ,x0+δ]
A cosa serve
La serie si basa sulla formula di Taylor.
E' utilizzata per approssimare il comportamento di una funzione f(x) derivabile nell'intorno di un punto tramite un polinomio Pn ottenuto da una serie numerica.
Il teorema di Taylor
Una funzione per essere sviluppabile in una serie di Taylor deve soddisfare il seguente teorema
Una funzione f(x) è sviluppabile in serie di Taylor con centro x0 se dato un valore δ>0, la funzione è derivabile infinite volte nell'intervallo [x0-δ,x0+δ] e se esiste un valore M tale che per ogni n $$ |f^{n}(x)| \le M \:\:\: \forall x \in [x_0-δ,x_0+δ], $$
La dimostrazione
La formula di Taylor è composta da una serie ridotta n-sima e da un resto Rn(x) detto resto di Peano.
$$ s_n + R_n(x) $$
Considerando anche il resto di Peano, la formula eguaglia la funzione f(x)
$$ f(x) = s_n + R_n(x) $$
Per ogni x dell'intervallo (x0-δ,x0+δ) con δ>0
Nota. Il resto di Peano Rn misura l'errore di approssimazione della funzione tramite la serie. $$ f(x) - s_n = R_n(x) $$
Per ipotesi la funzione f(x) è derivabile più volte in x0 ed è sempre compresa entro un valore massimo M
Sapendo che la stima del resto di Peano è
$$ |R_n(x)| \le M \cdot \frac{|x-x_0|^{n+1}}{(n+1)!} $$
Poiché (x-x0)<δ
$$ |R_n(x)| \le M \cdot \frac{|x-x_0|^{n+1}}{(n+1)!} \le M \cdot \frac{δ^{n+1}}{(n+1)!} $$
Per semplicità considero solo gli estremi della disequazione precedente
$$ |R_n(x)| \le M \cdot \frac{δ^{n+1}}{(n+1)!} $$
Calcolo il limite di entrambi i membri per n→∞
$$ \lim_{n \rightarrow \infty} |R_n(x)| \le \lim_{n \rightarrow \infty} M \cdot \frac{δ^{n+1}}{(n+1)!} $$
Essendo δ>0 l'ultimo limite tende a zero per n→∞
$$ \lim_{n \rightarrow \infty} |R_n(x)| \le 0 $$
Pertanto anche il valore assoluto del resto di Peano tende a zero per ogni x dell'intervallo (x0-δ,x0+δ).
$$ \lim_{n \rightarrow \infty} |R_n(x)| = 0 $$
Questo dimostra che la serie di Taylor sn(x) approssima la funzione f(x) nell'intorno (x0-δ,x0+δ).
$$ f(x) = s_n + R_n(x) $$
$$ f(x) - R_n(x) = s_n $$
Per n→∞ la serie di Taylor è uguale alla funzione f(x) nell'intorno (x0-δ,x0+δ).
$$ \lim_{n \rightarrow \infty} [ f(x) - R_n(x) ] = \lim_{n \rightarrow \infty} s_n $$
$$ f(x) = \lim_{n \rightarrow \infty} s_n $$
$$ f(x) = s_n \:\:\: con \: n=\infty $$
In conclusione, la funzione f(x) è sviluppabile in serie di Taylor nell'intervallo (x0-δ,x0+δ) con centro x0.
Un esempio pratico
Considero la funzione seno
$$ f(x) = \sin x $$
La funzione è derivabile infinite volte e ogni derivata è inferiore a un valore M≤1
Quindi, posso costruire la serie di Taylor della funzione.
Prendo in considerazione il punto x0=0.
Nota. Qualsiasi altro punto diverso da zero andrebbe bene. La scelta di x0=0 è per pura convenienza perché semplifica il calcolo della serie di Taylor. Quando la serie di Taylor è calcolata per x0=0 è anche detta serie di Mac Laurin.
Comincio con il primo termine k=0 della serie
$$ \frac{f^{(k)}(x_0)}{k!} (x-x_0)^k = \frac{ \sin 0}{0!} (x-0)^0 = 0 $$
Nota. La funzione f(k)(x0) è la derivata k-esima della funzione f(x) nel punto x0. Ad esempio, per k=0 si ha f(0)(x0)=f(x0), per k=1 si ha la derivata prima f(1)(x0)=f'(x0), per k=2 la derivata seconda f(2)(x0)=f''(x0). E così via.
Calcolo il secondo termine della serie k=1
$$ \frac{ \cos 0}{1!} (x-0)^1 = x $$
Calcolo il terzo termine della serie k=2
$$ \frac{ - \sin 0}{2!} (x-0)^2 = 0 $$
Calcolo il quarto termine della serie k=3
$$ \frac{ - \cos 0}{3!} (x-0)^3 = - \frac{x^3}{3!} $$
Calcolo il quinto termine della serie k=4
$$ \frac{ \sin 0}{4!} (x-0)^4 = 0 $$
Calcolo il sesto termine della serie k=5
$$ \frac{ \cos 0}{5!} (x-0)^5 = \frac{x^5}{5!} $$
Quindi fino a k=5 la serie di Taylor della funzione seno è
$$ \sin x = 0 + x - \frac{x^3}{3!} + 0 + \frac{x^5}{5!} $$
ossia
$$ \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} $$
Il polinomio nel membro di destra approssima la funzione f(x) nell'intorno del punto x0=0.
Ecco la rappresentazione grafica del polinomio di Taylor ( di colore nero ) e della funzione f(x)=sin x ( di colore rosso ) sul diagramma cartesiano.
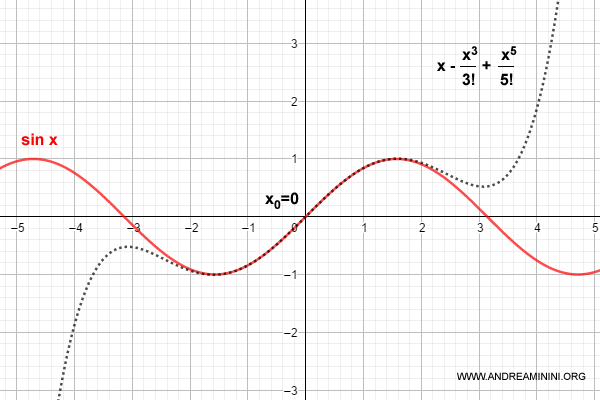
Come si può vedere dal grafico, il polinomio ricostruisce con discreta fedeltà la funzione f(x) nell'intorno di x0=0.
In particolar modo nell'intervallo da -2 a +2.
Nota. Se calcolassi la serie di Taylor più in profondita, per k=10 o k=20, il polinomio ricostruirebbe con maggiore fedeltà il grafico della funzione seno nell'intorno di x0=0 in un intervallo molto più ampio di (-2,2).
E così via
