Il numero di Nepero

Il numero di Nepero (e) è una costante matematica $$ e=2.71828182845904523536 $$ ed è alla base funzione esponenziale.

E' anche conosciuto come numero di Eulero.

La successione del numero di Nepero

Il numero di Nepero può essere stimato usando questa successione monotòna e limitata. $$ a_n = (1 + \frac{1}{n})^n $$

Questa successione è strettamente crescente e limitata. Pertanto converge a un numero reale per n->∞.

Il limite della successione per n tendente a infinito converge al numero di Nepero (e).

$$ \lim_{n \rightarrow ∞} 1 + \frac{1}{n} = e $$

Ecco la rappresentazione grafica della successione sul diagramma cartesiano

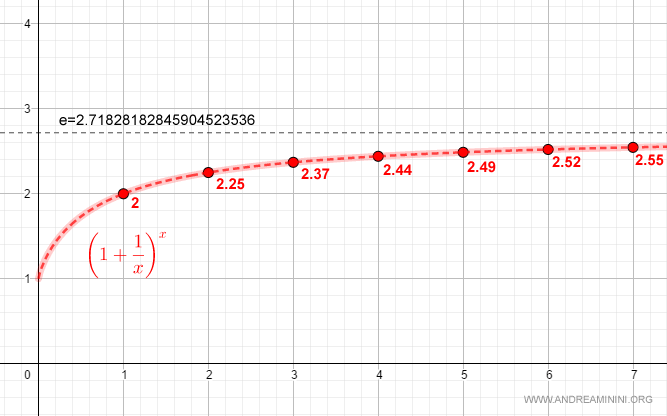
Dimostrazione

Riscrivo la successione di Nepero in questa forma equivalente

$$ \lim_{a_n \rightarrow +∞} (1 + \frac{1}{a_n})^{a_n} $$

Qualsiasi termine a_n della successione è maggiore o uguale rispetto al suo valore assoluto |a_n|

$$ |a_n| \le a_n $$

Ogni termine a_n è anche minore rispetto al suo valore assoluto |a_n|+1 più uno.

$$ |a_n| \le a_n < |a_n|+1 $$

Quindi, presi tre numeri qualsiasi b₁,b₂,b₃ che rispettano la diseguaglianza b₁<b₂<b₃ vale la seguente perché anche gli esponenti sono minori rispetto all'esponente successivo.

$$ b_1 ^{|a_n|} < b_2 ^{a_n} < b_3^{|a_n|+1} $$

Ora sostituisco b₁,b₂,b₃ con le seguenti:

$$ b_1 = 1 + \frac{1}{|a_n|+1} $$

$$ b_2 = 1 + \frac{1}{a_n} $$

$$ b_3 = 1 + \frac{1}{|a_n|} $$

Nota. I tre termini rispettano la diseguagianza. $$ b_1 < b_2 < b_3 $$ $$ 1 + \frac{1}{|a_n|+1} < 1 + \frac{1}{a_n} < 1 + \frac{1}{|a_n|} $$

Sostituisco b₁,b₂,b₃ nella diseguaglianza

$$ b_1 ^{|a_n|} < b_2 ^{a_n} < b_3^{|a_n|+1} $$

$$ (1 + \frac{1}{|a_n|+1})^{|a_n|} < (1 + \frac{1}{a_n})^{a_n} < (1 + \frac{1}{|a_n|})^{|a_n|+1} $$

Nota. La diseguaglianza è sempre soddisfatta perché sia le basi che gli esponenti sono minori rispetto alle successive.

Secondo la proprietà dei limiti anche i limiti delle successioni rispettano la diseguaglianza

$$ \lim_{a_n \rightarrow +∞} (1 + \frac{1}{|a_n|+1})^{|a_n|} < \lim_{a_n \rightarrow +∞} (1 + \frac{1}{a_n})^{a_n} < \lim_{a_n \rightarrow +∞} (1 + \frac{1}{|a_n|})^{|a_n|+1} $$

A questo punto analizzo il primo e il terzo membro della diseguaglianza.

Il primo membro è un limite notevole che tende al numero di Nepero.

$$ e < \lim_{a_n \rightarrow +∞} (1 + \frac{1}{a_n})^{a_n} < \lim_{a_n \rightarrow +∞} (1 + \frac{1}{|a_n|})^{|a_n|+1} $$

Scompongo in due il terzo membro

$$ e < \lim_{a_n \rightarrow +∞} (1 + \frac{1}{a_n})^{a_n} < \lim_{a_n \rightarrow +∞} (1 + \frac{1}{|a_n|})^{|a_n|+1} $$

$$ e < \lim_{a_n \rightarrow +∞} (1 + \frac{1}{a_n})^{a_n} < \lim_{a_n \rightarrow +∞} (1 + \frac{1}{|a_n|})^{|a_n|} \cdot (1 + \frac{1}{|a_n|}) $$

$$ e < \lim_{a_n \rightarrow +∞} (1 + \frac{1}{a_n})^{a_n} < \lim_{a_n \rightarrow +∞} (1 + \frac{1}{|a_n|})^{|a_n|} \cdot \lim_{a_n \rightarrow +∞} (1 + \frac{1}{|a_n|}) $$

$$ e < \lim_{a_n \rightarrow +∞} (1 + \frac{1}{a_n})^{a_n} < e \cdot 1 $$

$$ e < \lim_{a_n \rightarrow +∞} (1 + \frac{1}{a_n})^{a_n} < e $$

Pértanto, per il teorema del confronto dei limiti anche il secondo membro tende al numero di Nepero (e).

$$ \lim_{a_n \rightarrow +∞} (1 + \frac{1}{a_n})^{a_n} = e $$

Nota. Anche il limite della successione tendente a -∞ converge al numero di Nepero. La dimostrazione è simile alla precedente. $$ \lim_{a_n \rightarrow -∞} (1 + \frac{1}{a_n})^{a_n} = e $$

E così via.