La serie di MacLaurin
La serie di MacLaurin (o Mc Laurin) è una formula che approssima il comportamento di una funzione nell'intorno del punto x0=0. $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!} \cdot x^k + o(x^n) $$
Il polinomio che si ottiene tramite la formula è un'approssimazione di ordine n della funzione f(x) intorno a zero.
Quanto più è alto il grado n del polinomio di McLaurin, tanto più approssima meglio la funzione f(x).
Nota. La serie di MacLaurin è un caso particolare della formula di Taylor in cui x0=0. $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x-x_0)^k + R_n(x) $$
Un esempio pratico
Prendo in considerazione la funzione esponenziale
$$ f(x)=e^x $$
Il grafico della funzione esponenziale è
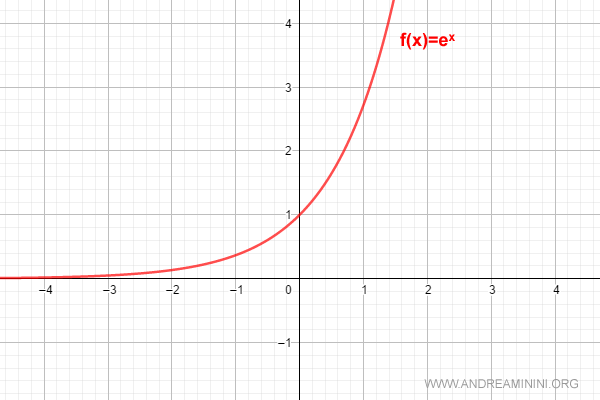
Provo a costruire un polinomio in grado di approssimare la funzione esponenziale con la formula di McLaurin.
$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!} \cdot x^k + o(x^n) $$
ossia
$$ P_n(x) = \sum_{k=0}^{n} \frac{D^{(k)}[e^0]}{k!} \cdot x^k + o(x^n) $$
Per n=0 la formula vale
$$ P_0(x) = \sum_{k=0}^{0} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 $$
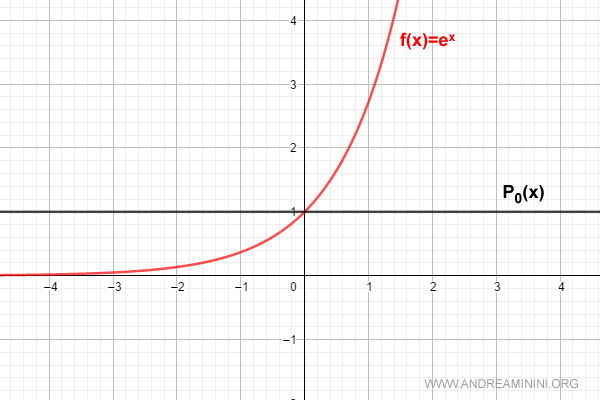
Per n=1 la formula vale
$$ f(x) = \sum_{k=0}^{1} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x $$
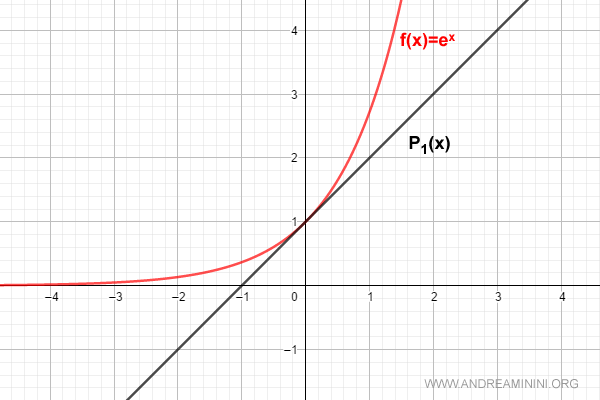
Per n=2 la formula vale
$$ f(x) = \sum_{k=0}^{2} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x + \frac{x^2}{2!} $$
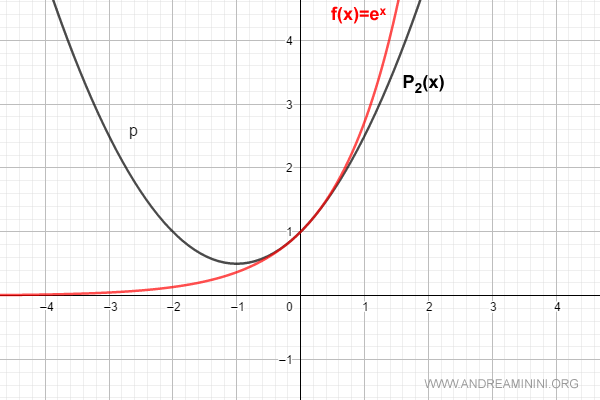
per n=3 la formula vale
$$ f(x) = \sum_{k=0}^{3} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} $$
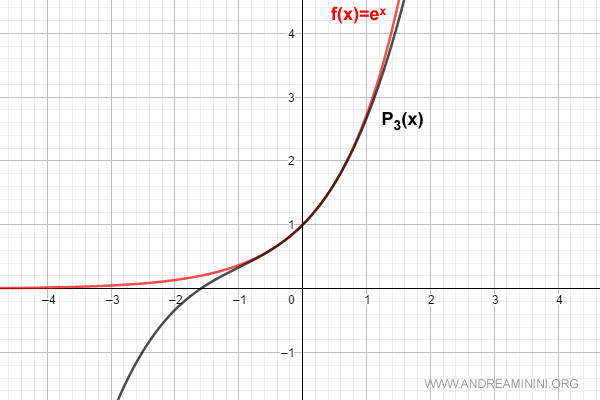
Man mano aumenta il grado del polinomio, la formula di MacLaurin approssima meglio la funzione nell'intorno di x0=0.
Ad esempio per n=9 il polinomio approssima molto bene la funzione nell'intorno di zero.
$$ f(x) = \sum_{k=0}^{9} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ... + \frac{x^9}{9!} $$
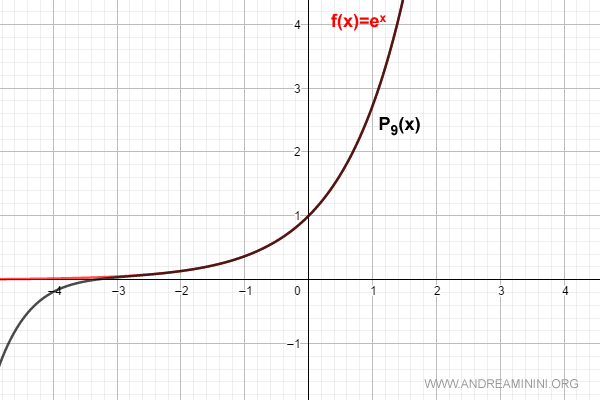
Quindi, per un qualsiasi numero intero n il polinomio è
$$ f(x) = \sum_{k=0}^{n} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ... + \frac{x^n}{n!} $$
E così via.
