Serie geometrica
La serie geometrica è la seguente: $$ \sum_{k=0}^{\infty} x^k = 1+x+x^2+...+x^k $$
Il carattere della serie geometrica dipende dal valore x detto ragione della serie geometrica
- x≥1 la serie diverge
- x<|1| la serie converge
- x≤-1 la serie è indeterminata/irregolare
Come calcolare la convergenza della serie geometrica. Quando la serie geometrica è convergente, ossia nei casi in cui la ragione è -1<x<1, la serie converge al numero finito $$ \sum_{k=0}^{\infty} x^k = \frac{1}{1-x} $$
Un esempio pratico
1] La ragione è maggiore di zero
Se la ragione è positiva (x>0) la serie è una serie non negativa
Quindi, per il teorema delle serie non negative, la serie ammette sicuramente un limite finito (serie convergente) o infinito (serie divergente).
A questo punto devo studiare due situazioni (x≥1 e 0<x<1).
Per x≥1 la serie diverge a infinito
Essendo una serie a termini non negativi, la serie non è indeterminata. Può essere convergente o divergente.
Calcolo il limite della successione del termine generale della serie per verificare se la condizione necessaria di convergenza è soddisfatta.
$$ \lim_{k \rightarrow \infty} x^k = + \infty \ne 0 $$
Il limite non tende a zero, quindi la serie non è convergente.
Quindi per esclusione è sicuramente una serie divergente se x≥1.
$$ \lim_{n \rightarrow \infty} \sum_{k=0}^{n} x^k = ± \infty $$
Esempio. Se la ragione è x=1.1 la serie è divergente perché il limite della successione non è uguale a zero.
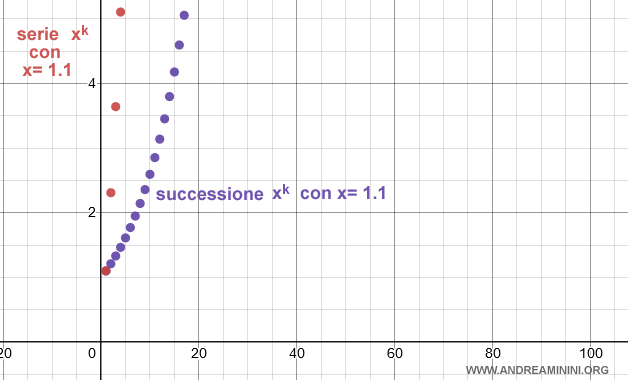
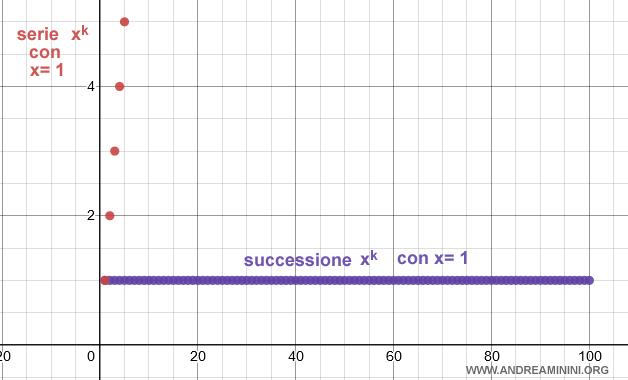
Se la serie è divergente, non necessariamente anche il limite della successione deve essere divergente. Ad esempio, se la ragione è x=1 la serie è comunque divergente perché il limite della successione non converge a zero ma a uno.
Per 0≤x<1 la serie converge
E' una serie a termini non negativi, quindi non è indeterminata. Può essere convergente o divergente.
Calcolo il limite della successione del termine generale della serie per verificare se la condizione necessaria di convergenza è soddisfatta.
$$ \lim_{k \rightarrow \infty} x^k = 0 $$
In questo caso la condizione necessaria (ma non sufficiente) di convergenza è soddifatta.
Quindi, non posso escludere che sia convergente. Potrebbe essere convergente o divergente.
Per studiare il comportamento della serie devo trovare un altro modo.
Posso riscrivere la serie armonica in questo modo:
$$ 1 + x + x^2 +x^3 + ... + x^n = \frac{1-x^{n+1}}{1-x} $$
Dimostrazione. Osservando i primi valori della serie armonica, le somme parziali sono equivalenti al rapporto (1-xn+1)/(1-x). $$ \sum_{n=0}^{\infty} x^n = \frac{1-x^{n+1}}{1-x} $$ Per dimostrare che la formula sia valida per tutti i valori n, ricorro al principio di induzione. La base con n=1 è soddisfatta. $$ P(1) \: := \: \sum_{k=0}^{1} x^k = \frac{1-x^{n+1}}{1-x} $$ $$ P(1) \: := \: \sum_{k=0}^{1} x^k = \frac{1-x^{1+1}}{1-x} $$ $$ P(1) \: := \: \sum_{k=0}^{1} x^k = \frac{1-x^{2}}{1-x} $$ $$ P(1) \: := \: \sum_{k=0}^{1} x^k = \frac{(1-x)(1+x)}{1-x} $$ $$ P(1) \: := \: \sum_{k=0}^{1} x^k = 1+x $$ Nell'ipotesi ritengo valida la formula per ogni n. $$ P(n) \: := \: \sum_{k=0}^{n} x^k = \frac{1-x^{n+1}}{1-x} $$ Quindi, verifico se anche il passo induttivo P(n+1) è verificato, aggiungendo xn+1 in entrambi i membri di P(n). $$ P(n+1) \: := \: [ \sum_{k=0}^{n} x^k ] + x^{n+1} = \frac{1-x^{n+1}}{1-x} + x^{n+1} $$ $$ P(n+1) \: := \: [ \sum_{k=0}^{n} x^k ] + x^{n+1} = \frac{1-x^{n+1}+(1-x) x^{n+1}}{1-x} $$ $$ P(n+1) \: := \: [ \sum_{k=0}^{n} x^k ] + x^{n+1} = \frac{1-x^{n+1}+x^{n+1}-x \cdot x^{n+1}}{1-x} $$ $$ P(n+1) \: := \: [ \sum_{k=0}^{n} x^k ] + x^{n+1} = \frac{1- x^{n+2}}{1-x} $$ Il passo induttivo è verificato. Quindi, l'ipotesi è vera e la formula è valida per ogni n∈N.
Pertanto, il limite della serie geometrica
$$ \lim_{n \rightarrow \infty} \sum_{k=0}^{n} x^k $$
posso riscriverlo usando la formula appena trovata
$$ \lim_{n \rightarrow \infty} \frac{1-x^{n+1}}{1-x} $$
Essendo 0<x<1 il termine xn+1 tende a zero per n→∞.
Pertanto il limite è convergente
$$ \lim_{n \rightarrow \infty} \frac{1-x^{n+1}}{1-x} = \frac{1}{1-x} $$
Ne consegue che anche la serie geometrica converge a 1/1-x
$$ \lim_{n \rightarrow \infty} \sum_{k=0}^{n} x^k = \frac{1}{1-x} $$
E' una serie convergente
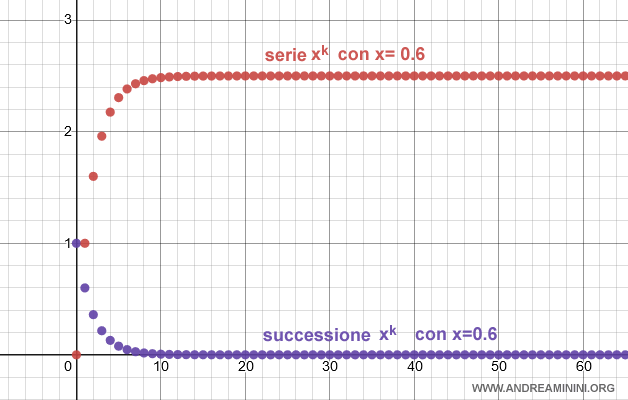
Esempio. Se la ragione è x=0.6 la serie è convergente perché la successione dei termini 0.6k tende a zero per k→∞. La serie converge a $$ \sum_{k=0}^{\infty} x^k = \frac{1}{1-0.6} = 2.5 $$ Ecco la rappresentazione grafica della serie e della successione sul diagramma cartesiano.
2] La ragione è minore o uguale a zero
Se la ragione è negativa (x<0) non posso più usare il teorema delle serie non negative.
Quindi, non posso escludere che la serie sia indeterminata. Devo studiare la serie in qualche altro modo.
Posso riscrivere la serie armonica in questo modo:
$$ 1 + x + x^2 +x^3 + ... + x^n = \frac{1-x^{n+1}}{1-x} $$
A questo punto distinguo due situazioni possibili.
Per -1<x≤0 la serie converge
Il limite della serie geometrica
$$ \lim_{n \rightarrow \infty} \sum_{k=0}^{n} x^k $$
posso riscriverlo usando la formula appena trovata
$$ \lim_{n \rightarrow \infty} \frac{1-x^{n+1}}{1-x} $$
Poiché x<|1| il termine xn+1 al denominatore tende a zero
$$ \lim_{n \rightarrow \infty} \sum_{k=0}^{n} x^k = l_f $$
$$ \lim_{n \rightarrow \infty} \frac{1-x^{n+1}}{1-x} = \frac{1}{1-x} $$
Pertanto, la serie converge al numero reale finito 1/1-x
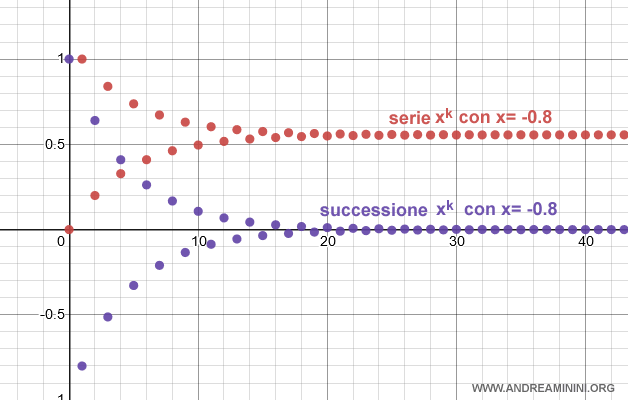
Esempio. La serie geometrica con ragione x=-0.8 è convergente perché il limite della successione dei termini tende a zero. La serie converge a $$ \sum_{k=0}^{\infty} x^k = \frac{1}{1-(-0.8)} = 0.55 $$ Pur essendo oscillante, la serie converge a un numero finito per k tendente a infinito. Ecco la rappresentazione grafica.
Per x≤-1 la serie è non regolare (indeterminata)
Il limite della serie geometrica
$$ \lim_{n \rightarrow \infty} \sum_{k=0}^{n} x^k $$
posso riscriverlo usando la formula appena trovata
$$ \lim_{n \rightarrow \infty} \frac{1-x^{n+1}}{1-x} $$
In questi caso x≤-1, quindi il termine xn+1 tende +∞ se n è dispari e -∞ se n è pari.
Ne consegue che il limite è indeterminato.
$$ \lim_{n \rightarrow \infty} \frac{1-x^{n+1}}{1-x} = \: ind $$
Pertanto se x≤-1 la serie geometrica è una serie non regolare.
Esempio. Se la ragione della serie geometrica è x=-1.1 la serie è indeterminata, perché non esiste il limite della successione dei termini. Sia la successione che la serie sono oscillanti.
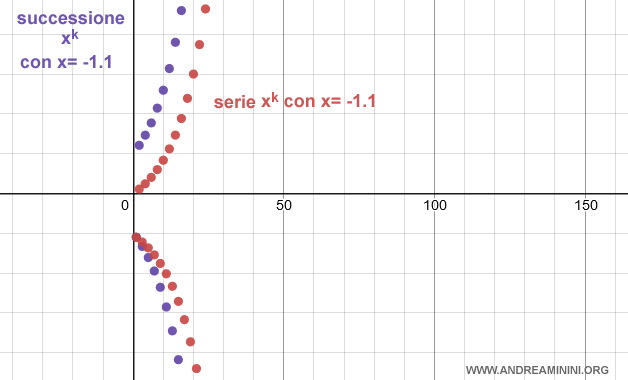
Lo stesso accade se la ragione della serie geometrica è x=-1.
E così via
