Gruppi simmetrici

Un gruppo simmetrico (S_n,*) di un insieme S è un gruppo formato dall'insieme S_n delle permutazioni degli elementi dell'insieme S e dall'operazione binaria di composizione di funzioni f*g=f o g=f[g)]

Dove ogni permutazione posso considerarla come una funzione o corrispondenza biunivoca σ dell'insieme S e se stesso.

$$ \sigma : S \rightarrow S $$

L'insieme S_n è l'insieme di tutte le corrispondenze biunivoche tra l'insieme S e se stesso.

$$ S_n = \{ \sigma_1, \sigma_2 , ... , \sigma_k \} $$

Il gruppo simmetrico (S_n,*) è un gruppo di ordine k=n! perché esistono n! permutazioni possibili tra n elementi dell'insieme finito S.

Nota. I gruppi simmetrici di insiemi finiti con la stessa cardinalità (n elementi) sono isomorfi. Inoltre, tutti i gruppi di insiemi con cardinalità maggiore di due sono gruppi non abeliani (non commutativi).

Un esempio pratico

Considero un insieme con tre elementi (n=3)

$$ S = \{ 1,2,3 \} $$

Esistono n!=3·2·1=6 permutazioni possibili tra gli elementi

$$ S_n = \begin{Bmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \\ 2 & 1 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \\ 3 & 2 & 1 \end{Bmatrix} $$

Se l'insieme iniziale è S={1,2,3} una corrispondenza biunivoca σ (permutazione) è la seguente

$$ \sigma : (1,2,3) \rightarrow (2,3,1) $$

Per scrivere la corrispondenza biunivoca σ utilizzo la notazione tabellare

$$ \sigma = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$

Ogni colonna della matrice è una relazione S→S tra l'insieme S e se stesso

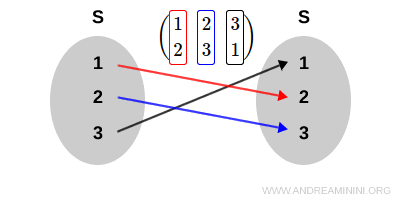
Nota. La corrispondenza σ agisce in questo modo $$ \sigma : 1 \rightarrow 2 \\ \sigma : 2 \rightarrow 3 \\ \sigma : 3 \rightarrow 1 $$ La corrispondenza è biunivoca. Ad esempio, σ(1)=3 in quanto 1→2 e 2→3 e σ(3)=1 in quanto 3→1.

L'insieme delle corrispondenze biunivoche σ forma un gruppo simmetrico (S_n,*) rispetto all'operazione di composizione *.

$$ (S_n, *) $$

Nota. Il gruppo simmetrico (S_n,*) è di ordine n!=6 perché l'insieme delle permutazioni S_n è composto da 6 elementi (cardinalità di S_n). $$ S_n = \begin{Bmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \\ 2 & 1 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \\ 3 & 2 & 1 \end{Bmatrix} $$

L'operazione di composizione * un'operazione binaria tra due corrispondenze biunivoche (permutazioni) ossia tra due elementi di S_n

Ad esempio, considero due corrispondenze biunivoche

$$ \sigma_1 : (1,2,3) \rightarrow (2,1,3) = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} $$

$$ \sigma_2 : (1,2,3) \rightarrow (2,3,1) = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$

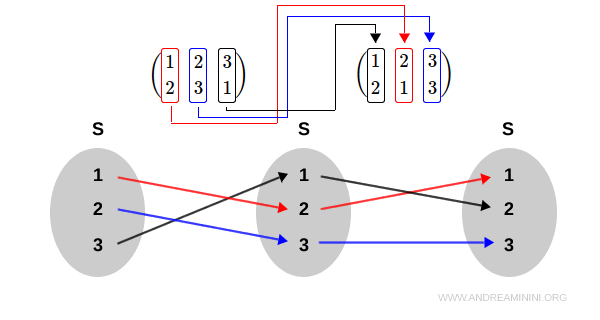
Un'operazione di composizione delle corrispondenze biunivoche (permutazione) è la seguente

$$ \sigma_1 * \sigma_2 = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} * \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} \ $$

Essendo un'operazione di composizione f*g=f[g] dove g= σ₂ e f= σ₁ devo svolgere il calcolo da destra verso sinistra, ossia dalla funzione più interna a quella più esterna.

$$ \sigma_1 * \sigma_2 = \sigma_1 [ \sigma_2 ] = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} * \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} \ $$

In pratica, devo partire dalla permutazione σ₂ perché è il dominio della permutazione σ₁

In questo caso il risultato dell'operazione di composizione è (1,3,2)

$$ \sigma_1 * \sigma_2 =\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} * \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix} $$

Un'analisi grafica dovrebbe rendere più chiari tutti i passaggi

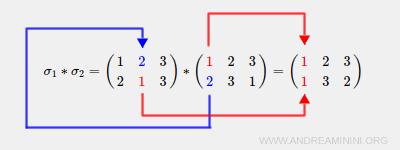
Spiegazione. La corrispondenza biunivoca σ₂ (funzione interna g) associa 1→2 mentre σ₁ (funzione esterna f) associa 2→1. Quindi, l'operazione di composizione σ₁*σ₂ associa 1→1.

La corrispondenza biunivoca σ₂ associa 2→3 mentre σ₁ associa 3→3. Quindi, l'operazione di composizione σ₁*σ₂ associa 2→3.

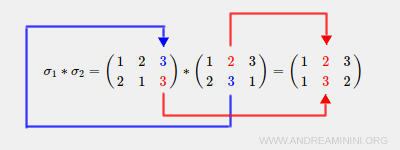
La corrispondenza biunivoca σ₂ associa 3→1 mentre σ₃ associa 1→2. Quindi, l'operazione di composizione σ₁*σ₂ associa 3→2.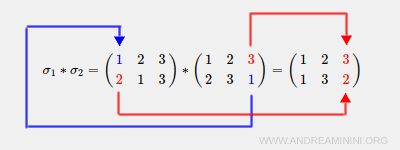

E' un gruppo abeliano o non abeliano?

Il gruppo simmetrico (S_n,*) è formato dalle permutazioni degli elementi dell'insieme S rispetto all'operazione di composizione.

Il gruppo S ha cardinalità n=3.

Quindi, avendo S una cardinalità maggiore di due (n>2) il gruppo simmetrico è sicuramente un gruppo non abeliano, ossia non soddisfa la proprietà commutativa.

Verifica. Per verificare quest'ultima affermazione riprendo la composizione precedente che dà come risultato la permutazione (1,3,2) $$ \sigma_1 * \sigma_2 =\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} * \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 \\ \color{red} 1 & \color{red} 3 & \color{red} 2 \end{pmatrix} $$ Se inverto l'ordine della composizione ottengo un risultato diverso ossia (3,2,1) $$ \sigma_2 * \sigma_1 =\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} * \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 \\ \color{red} 3 & \color{red} 2 & \color{red} 1 \end{pmatrix} $$ Pertanto, il gruppo (S_n,*) non soddisfa la proprietà commutativa $$ \sigma_1 * \sigma_2 \ne \sigma_2 * \sigma_1 $$ E' un gruppo non abeliano.

E così via