Logaritmi discreti
Il logaritmo discreto è una versione del logaritmo classico che si calcola quando si lavora con numeri interi in un campo finito o un gruppo finito.
Più formalmente, se \( G \) è un gruppo ciclico di ordine \( n \) e \( g \) è un generatore di \( G \), allora per ogni elemento \( a \) in \( G \), il logaritmo discreto \( x \) è un numero intero tale che:
\[ g^x \equiv a \mod n \]
dove \( x \) si trova nell'intervallo da \( 0 \) a \( n-1 \).
Ogni elemento di \( G \) può essere scritto come \( g^k \) per qualche intero \( k \).
Il logaritmo discreto di un elemento \( a \) in base \( g \) denotato come logg(a) è il valore \( x \) tale che \( g^x = a \) è all'interno del gruppo.
A cosa serve? E' particolarmente utilizzato nella teoria dei numeri e crittografia. Il calcolo dei logaritmi discreti è noto per essere computazionalmente difficile, il che lo rende una funzione "a senso unico" adatta per la crittografia, perché mentre è computazionalmente facile calcolare gx nel modulo n, il processo inverso di trovare x in un'equazione del tipo gx=y mod n ovvero il logaritmo discreto x=logg(y) mod n è molto difficile. Questa asimmetria è alla base di molti schemi crittografici.
Un esempio pratico
Considero un gruppo ciclico su un campo finito di 11 elementi, dove l'aritmetica è definita modulo 11.
$$ G = (1,2,3,4,5,6,7,8,9,10,11) $$
Il che significa che 10+1 (mod 11) è uguale a 11 ma 11+1 (mod 11) è uguale a 1, perché il calcolo riparte dalla prima posizione.
Anche in questo gruppo posso calcolare la potenza degli elementi:
$$ 2^1 \mod 11 = 2 $$
$$ 2^2 \mod 11 = 4 $$
$$ 2^3 \mod 11 = 8 $$
$$ 2^4 \mod 11 = 5 $$
Nota. La potenza 24 = 16 nell'insieme dei numeri interi ma 16 non è compreso nel gruppo modulo 11. Quindi, per dirla in modo semplice 16-11=5.
Diciamo che ora voglio cercare il logaritmo discreto di 9 in base 2 modulo 11, che è l'ora corrispondente \( x \) tale che
$$ 2^x \equiv 9 \mod 11 $$
Per risolvere questo, devo trovare x tale che \( 2^x \) dia 9 quando considerato modulo 11.
Procedo per tentativi perché sto usando numeri molto piccoli e questo è fattibile:
$$ 2^1 \mod 11 = 2 $$
$$ 2^2 \mod 11 = 4 $$
$$ 2^3 \mod 11 = 8 $$
$$ 2^4 \mod 11 = 5 $$
$$ 2^5 \mod 11 = 10 $$
$$ 2^6 \mod 11 = 9 $$
Quindi, il logaritmo discreto di 9 in base 2 modulo 11 è 6.
Verifica. In effetti 26=64 nei numeri reali. Nell'aritmetica modulo 11 il numero 64 equivale a 9. Per verificarlo basta costruire la tabella moltiplicativa del gruppo ciclico. La moltiplicazione 8x8 modulo 11 dà come risultato il numero 9. Quindi, il risultato è corretto.
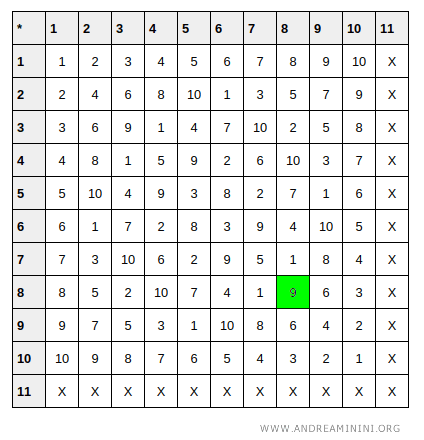
Questo esempio mostra come funziona il logaritmo discreto-
Inoltre, dimostra come, anche se è relativamente semplice verificare che \( 2^6 = 9 \mod 11 \), trovare il valore \( x \) può diventare un compito arduo, soprattutto con numeri molto più grandi, come quelli utilizzati nella crittografia.
E così via.
