La matrice quadrata
La matrice quadrata è una matrice con lo stesso numero di righe e di colonne ( m=n ). E' detta matrice di ordine n ed è indicata con il simbolo A(n).
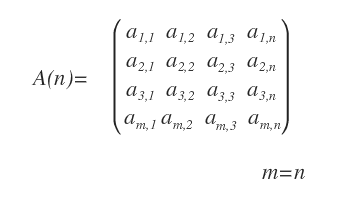
A cosa servono le matrici quadrate? Le matrici quadrate hanno caratteristiche e proprietà specifiche rispetto alle altre che le rendono particolarmente utili nell'algebra lineare.
La diagonale della matrice quadrata
Le matrici quadrate sono caratterizzate dalla presenza di due diagonali.
- La diagonale principale. Data una matrice quadrata di ordine n, la diagonale principale è composta dagli elementi ai,i per i = 1 , ... , n. E' la diagonale discendente che parte in alto a sinistra e finisce in basso a destra.

- La diagonale secondaria. Data una matrice quadrata di ordine n, la diagonale secondaria è composta dagli elementi ai,i per i = n , ... , 1. E' la diagonale che parte in alto a destra e finisce in basso a sinistra.

Nota. Le matrici quadrate sono le uniche matrici ad avere delle diagonali. Le matrici rettangolari, matrici riga, matrici colonna e matrici nulle non hanno nessuna diagonale.
Le matrici diagonali, triangolari superiori e inferiori
In particolari situazioni le matrici quadrate sono dette diagonali, triangolari superiori o inferiori
- Triangolare superiore. La matrice è detta triangolare superiore se aij = 0 per ogni i>j. Se sono uguali a zero tutti gli elementi al di sotto della diagonale principale.

L'insieme delle matrici reali triangolari superiori di ordine n è indicato con Un(R).Strettamente triangolare superiore. La matrice è detta strettamente triangolare superiore se sono uguali a zero tutti gli elementi aij per ogni i≥j, ossia gli elementi della diagonale principale e tutti gli elementi al di sotto della diagonale principale.

Una matrice strettamente triangolare superiore è anche triangolare superiore. L'insieme delle matrici reali strettamente triangolari superiori di ordine n è indicato con U*n(R). - Triangolare inferiore. La matrice è detta triangolare inferiore se aij = 0 per ogni i<j. Se sono uguali a zero tutti gli elementi al di sopra della diagonale principale.

L'insieme delle matrici reali triangolari inferiori di ordine n è indicato con Ln(R).Strettamente triangolare inferiore. La matrice è detta strettamente triangolare inferiore se sono uguali a zero tutti gli elementi aij per ogni i≤j, ossia gli elementi della diagonale principale e tutti gli elementi al di sopra della diagonale principale.

Una matrice strettamente triangolare inferiore è anche triangolare inferiore. L'insieme delle matrici reali strettamente triangolari inferiori di ordine n è indicato con L*n(R). - Diagonale. La matrice quadrata è detta diagonale se aij = 0 per ogni i≠j. Se sono uguali a zero tutti gli elementi al di sopra e al di sotto della diagonale principale. In pratica, una matrice diagonale è sia triangolare superiore che triangolare inferiore.
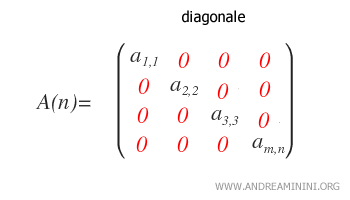
L'insieme delle matrici reali diagonali di ordine n è indicato con Dn(R).
Attenzione. La definizione di triangolare superiore o inferiore non implica che gli altri elementi debbano essere diversi da zero.
Casi particolari di matrici quadrate
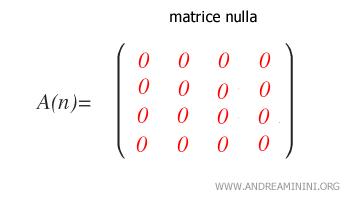
La matrice nulla è un caso particolare di matrice quadrata perché è contemporaneamente sia triangolare inferiore e superiore, sia strettamente triangolare inferiore e superiore, sia diagonale.
Un altro caso particolare è la matrice quadrata di ordine 1 perché è composta da un solo elemento a1,1.
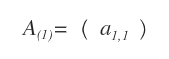
Per definizione la matrice quadrata di ordine 1 è sempre triangolare inferiore, triangolare superiore e diagonale.
Nota. Nel caso in cui a1,1 = 0, la matrice quadrata di ordine 1 è anche strettamente triangolare inferiore e superiore.

