La potenza di matrice
La potenza di una matrice si ottiene tramite la moltiplicazione righe per colonne della matrice per se stessa.
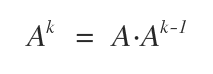
Data una matrice quadrata A di ordine n e un numero intero non negativo k , la potenza Ak è uguale al prodotto ricorsivo della matrice A per se stessa per k-1 volte.
Attenzione. La potenza della matrice non è l'elevazione a potenza degli elementi della matrice. Questo si verifica solo in alcune circostanze come nelle matrici diagonali.
Un esempio di potenza di matrice
Ho la seguente matrice quadrata A di ordine 2 e voglio calcolare l'elevazione al cubo.
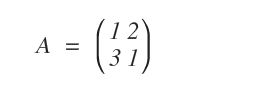
Per calcolare la potenza cubica della radice devo moltiplicare la matrice per se stessa per tre volte.
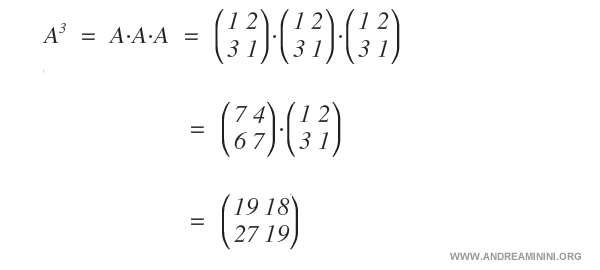
Nota. Come si può notare la potenza A3 non conduce a una matrice con elementi elevati alla terza perché la moltiplicazione matriciale righe per colonne è un procedimento con proprietà differenti rispetto al prodotto fra numeri reali.
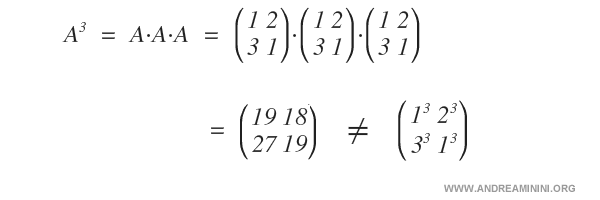
Le matrici nilpotenti e idempotenti
Una matrice quadrata A di ordine n è detta nilpotente di ordine k se la potenza Ak è una matrice nulla (O).
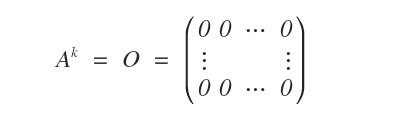
Ecco un esempio di matrice nilpotente.
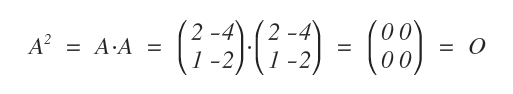
Una matrice quadrata A di ordine n è detta idempotente di ordine k se la potenza Ak è uguale a A.

Ecco un esempio pratico di matrice idempotente:
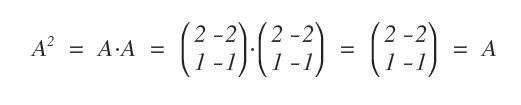
Nota. Le matrici nilpotenti e idempotenti sono risultati possibili soltanto nella moltiplicazione riga per colonna tra matrici.
La potenza zero della matrice
Una qualsiasi matrice quadrata di ordine n elevata a zero dà come risultato una matrice unitaria I di ordine n.
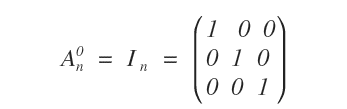
La potenza della matrice con esponente negativo
Se l'esponente k della potenza è negativo, la potenza della matrice A si calcola moltiplicando per k volte la sua matrice inversa A-1.
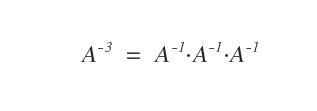
Il caso delle matrici diagonali
Le matrici diagonali sono l'unico caso in cui la potenza della matrice coincide alla potenza dei singoli elementi.
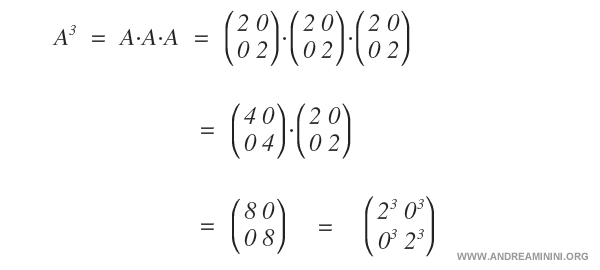
Si tratta comunque di un caso particolare.
In tutti gli altri casi, la potenza di una matrice non coincide necessariamente con la potenza degli elementi.
Il caso della potenza del binomio di matrici
Nel caso delle matrici non vale la regola della potenza del binomio dei numeri reali.
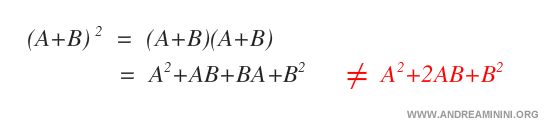
Nota. E' un altro esempio della particolarità della potenza tra matrici che non va confusa con la potenza dei numeri reali, perché segue un procedimento di calcolo differente.
