La moltiplicazione di una matrice per uno scalare

Il prodotto di una matrice B con un numero reale α ( scalare ) è una matrice B' con gli elementi corrispondenti di b_ij moltiplicati per α ( α·b_ij ).

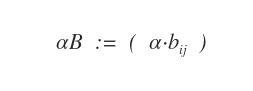
Un esempio pratico. In questo esempio moltiplico lo scalare α=3 per una matrice A. Il risultato finale è la matrice A con tutti gli elementi moltiplicati per tre.

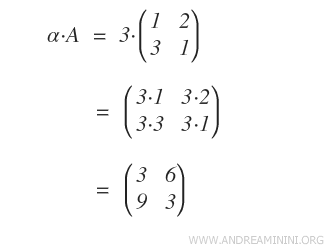
Le proprietà della moltiplicazione

Il prodotto del numero reale e di una matrice rispetta le seguenti proprietà:

1. Distribuzione rispetto alla somma di matrici
   Il prodotto α·(A+B) è uguale alla somma α·A + α·B.

   Nota. Dove A e B sono due matrici mentre α è un numero reale.

2. Distribuzione rispetto alla somma di scalari
   Il prodotto (α+β)·A è uguale alla somma α·A + β·A.
3. Compatibilità del prodotto
   Il prodotto (α·β)·A è uguale al prodotto α·(β·A)
4. Esistenza dell'elemento neutro
   Il prodotto tra il numero uno e una matrice dà come risultato la matrice stessa 1·A=A. Quindi, il numero uno è l'elemento neutro.
5. Prodotto per l'elemento neutro
   Il prodotto tra lo zero e una matrice dà come risultato una matrice nulla ( 0·A=O ).
6. Compatibilità dell'elemento opposto
   Il prodotto tra -1 e la matrice dà come risultato la matrice opposta. (-1)·A=-A