La relazione riflessiva
Cosa sono le relazioni riflessive
Una relazione definita in un insieme A è riflessiva se ogni elemento a di A è in relazione con se stesso. $$ \forall \ a \in \ A \ , \ aRa $$
Nelle relazioni riflessive ogni elemento dell'insieme è collegato con con se stesso.
Ad esempio, la relazione "X ha la stessa età di Y" è riflessiva perché qualsiasi X ha la stessa età di se stesso.
Le relazioni riflessive sono un sottoinsieme delle relazioni definite in un insieme.
Un esempio pratico
Considero l'insieme A
$$ A = \{ 2,3,4,5,6,7,8,9 \} $$
La relazione R collega ogni elemento dell'insieme A con i suoi multipli presenti nello stesso insieme.
$$ R = \{ (2;2) , (2;4),(2;6),(2;8),(3;3),(3;6),(3;9)\\ \ \ \ \ \ \ \ \ \ \ \ \ (4;4) , (4;8),(5;5),(6;6),(7;7),(8;8),(9;9) \} $$
La relazione è un sottoinsieme del prodotto cartesiano AxA dell'insieme per se stesso.
Rappresento la relazione con una tabella a doppia entrata.
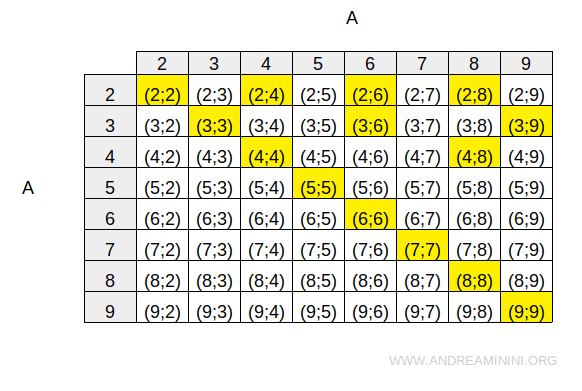
Le celle in giallo sono le coppie del prodotto cartesiano AxA che soddisfano la relazione R
Come si può notare ogni elemento è in relazione con se stesso.
La diagonale principale della tabella è composta esclusivamente da coppie ordinate appartenenti alla relazione (di colore giallo). Ad esempio (2;2), (3;3), (4;4), ecc.
Pertanto, la relazione R è una relazione riflessiva.
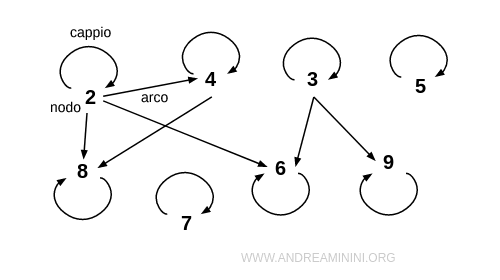
Nota. Nella rappresentazione tramite i grafi una relazione è riflessiva quando ogni nodo ha un cappio, ossia un collegamento con se stesso. In questo caso mi basta un colpo d'occhio per accorgermi se la relazione è riflessiva oppure no.
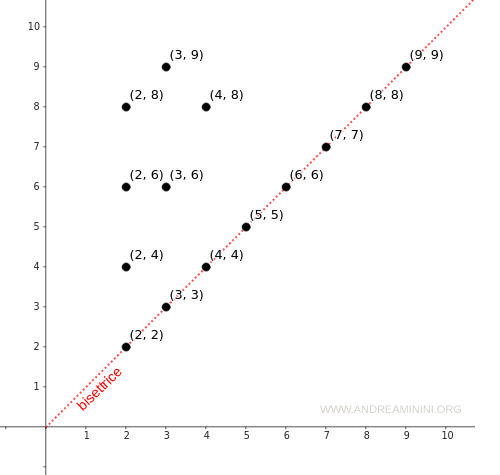
Nella rappresentazione cartesiana, invece, una relazione è riflessiva se tutti gli elementi dell'insieme A formano una coppia sulla bisettrice tramite la relazione R. Anche in questo caso una relazione riflessiva è facilmente individuabile a colpo d'occhio.
Altri esempi
- La relazione "x è perpendicolare a y" NON è riflessiva perché nessuna retta x può formare un angolo di 90° con se stessa.
E così via.
