La relazione transitiva
Cosa sono le relazioni transitive
Una relazione è transitiva quando, dati tre elementi qualsiasi a,b,c dell'insieme I, se a è in relazione con b e b è in relazione con c, allora a è in relazione con c. $$ \forall \ a,b,c \in I \ | \ aRb \ , \ bRc \ \Rightarrow aRc $$ Dal punto di vista grafico
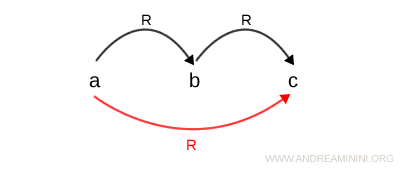
Sono dette transitive perché soddisfano la proprietà transitiva.
Ad esempio, se A è fratello di B e B è fratello di C, allora A è fratello di C.
Le relazioni transitive sono un sottoinsieme delle relazioni definite in un insieme.
Nota. La transitività è una proprietà soddisfatta da alcune relazioni ma non da tutte. Ad esempio, la relazione A è madre di B e B è madre di C non è transitiva.
Un esempio pratico
Considero l'insieme I
$$ I = \{ 2 , 4, 6,8,10 \} $$
La relazione R mette in relazione un coppia di numeri pari.
Gli elementi 2 e 4 sono in relazione tra loro perché sono entrambi pari.
$$ 2R4 $$
Anche gli elementi 4 e 6 sono in relazione tra loro perché sono entrambi pari.
$$ 4R6 $$
Per la proprietà transitiva anche gli elementi 2 e 6 sono in relazione tra loro, perché se 2 e 4 formano una coppia di numeri pari e 4 e 6 formano un'altra coppia di numeri pari, allora anche 2 e 6 formano una coppia di numeri pari.
$$ 2R6 $$
In questo caso la proprietà transitiva è soddisfatta per qualsiasi combinazione di elementi dell'insieme I={2,4,6,8,10}.
Pertanto, la relazione R è una relazione transitiva nell'insieme I.
Nota. Per rappresentare le relazioni transitive si usano i grafi. La proprietà transitiva in un grafo è subito evidente tramite i collegamenti tra i nodi (elementi dell'insieme). Se una freccia collega 2 a 4 e una freccia collega 4 a 6, allora c'è anche un'altra freccia che collega direttamente 2 a 6.
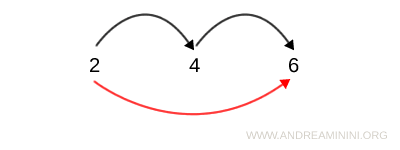
Viceversa, le tabelle a doppia entrata e i diagrammi cartesiani non evidenziano la proprietà riflessiva.
Altri esempi
- La relazione "x è perpendicolare a y" NON è transitiva perché se una retta x forma un angolo di 90° (angolo retto) con la retta y e la retta y forma un angolo di 90° (angolo retto) con la retta z, allora la retta x e la retta z formano un angolo di 180° (angolo piatto) oppure nullo. In entrambi i casi le rette x e z non sono perpendicolari.
E così via.
