Relazioni di preordine

Una relazione di preordine è anche detta relazione di "quasiordine" e questo fa già capire che si tratta di un insieme più ampio delle relazioni d'ordine.

A differenza di una relazione d'ordine, una relazione di preordine non richiede la proprietà di antisimmetria.

In una relazione di preordine, \( a \leq b \) e \( b \leq a \) non implicano che \( a \) e \( b \) siano identici, possono anche essere considerati equivalenti sotto la relazione ma rimanere distinti come elementi.

Viceversa, in una relazione d'ordine, se \( a \leq b \) e \( b \leq a \), allora necessariamente sono indentici \( a = b \). 

Nota. Il fatto che non ci sia la proprietà antisimettrica non vuole dire che la relazione d'ordine sia asimettrica. In altre parole, una relazione di preordine non è necessariamente antisimmetrica, potrebbe esserlo oppure no. Viceversa, in una relazione asimmetrica l'assenza della simmetria è una condizione necessaria. In una relazione antisimmetrica la simmetria è ammessa solo tra gli stessi elementi. I concetti di asimmetria e antisimmetria sono distinti.

A cosa serve una relazione di preordine?

Le relazioni di preordine sono utili per organizzare e relazionare elementi in base a criteri specifici, perché consentono l'equivalenza funzionale tra elementi distinti senza richiedere una equivalenza identitaria stretta.

Ad esempio, le preferenze di un consumatore sono relazioni di preordine. Un consumatore potrebbe preferire il caffè al té $ A \succ B $ (o viceversa $ A \prec B $) ma potrebbe anche essere indifferente tra il bere il caffé o il té $ A \sim B $, senza che questi ultimi siano la stessa cosa. Pertanto, le preferenze del consumatore non possono essere una relazione d'ordine. In una relazione d'ordine la relazione di indifferenza è ammessa solo tra elementi uguali (a=a) mentre in una relazione di preordine anche tra elementi diversi (a≠b) come il caffé e il té.

Un esempio pratico

Considero un insieme formato da quattro elementi, ogni elemento è un progetto.

$$ S = \{ A, B, C, D \} $$

Introduco una relazione di preordine tra i vari progetti.

 \(A \rightarrow B\): Il progetto \(A\) deve essere completato prima di \(B\).
 \(A \rightarrow C\): Il progetto \(A\) deve essere completato prima di \(C\).
 \(B \rightarrow D\): Il progetto \(B\) deve essere completato prima di \(D\).
 \(C \rightarrow D\): Il progetto \(C\) deve essere completato prima di \(D\).
 \(B \rightarrow C\): I progetti \(B\) e \(C\) hanno una relazione di collaborazione dove il lavoro su \(B\) può influenzare direttamente \(C\).
  \(C \rightarrow B\): Il progetto \(C\) può anche influenzare direttamente il progetto \(B\), rendendo la loro relazione bidirezionale e non più unilaterale.

Questa relazione soddisfa la proprietà riflessiva e transitiva

• Riflessività: Ogni progetto è presupposto completabile indipendentemente.
• Transitività: Se il progetto \(A \rightarrow B\) e \(B \rightarrow D\), allora implicitamente \(A \rightarrow D\).

Non è invece richiesta l'antisimmetria. Questo significa che due elementi dell'insieme possono essere in relazione biunivoca tra loro senza essere necessariamente lo stesso elemento.

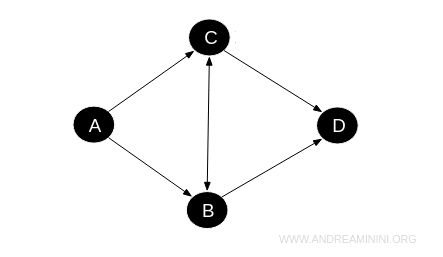
Ad esempio, la relazione tra \(B\) e \(C\) è bidirezionale (\(B \rightarrow C\) e \(C \rightarrow B\)), indicando che questi progetti possono essere considerati funzionalmente equivalenti o intercambiabili in alcuni contesti, senza che uno debbano essere lo stesso progetto.

In questo esempio, la relazione ciclica tra \(B\) e \(C\) rompe la proprietà di antisimmetria che è necessaria in una categoria poset (insieme parzialmente ordinati), facendola diventare una categoria preordinata.

Nota. Alcuni progetti possono avere interdipendenze complesse che non seguono una gerarchia lineare stretta, ma piuttosto permettono iterazioni e influenze reciproche.

E così via.