La relazione antisimmetrica

Cosa sono le relazioni antisimmetriche

Una relazione è antisimmetrica in un insieme X se, dati due elementi diversi tra loro, per ogni elemento a in relazione con b, l'elemento b non è in relazione con a. $$ a R b \ , \ a \ne b \ \Rightarrow b \require{cancel} \cancel{R} a $$

Nelle relazioni antisimmetriche non ci sono collegamenti biunivoci tra gli elementi.

Ad esempio, la relazione A "è maggiore-uguale" di B è antisimmetrica, perché se A è maggiore-uguale di B, allora B non può essere in maggiore uguale di A.

A parte il caso, ammesso in una relazione antisimmetrica, che A e B siano identici.

La differenza tra relazioni antisimmetriche e asimmetriche. Le relazioni antisimmetriche e asimmetriche sono concetti distinti, anche se possono sembrare simili in certi contesti. In una relazione antisimmetrica, le relazioni tra elementi diversi sono unidirezionali. In una relazione asimmetrica, invece, tutte le relazioni sono unidirezionali, quindi anche quelle tra gli stessi elementi. Ad esempio, la relazione "maggiore-uguale di" è antisimmetrica perché se A≥B e A≠B allora non può verificarsi che B≥A, in quanto i confronti tra gli stessi elementi sono esclusi. D'altra parte, la stessa relazione non è asimmetrica perché se A≥B quando A=B si verifica anche B≥A. Quindi, la relazione diventa bidirezionale.

Le relazioni antisimmetriche sono un sottoinsieme delle relazioni definite in un insieme.

Un esempio pratico

Considero l'insieme

$$ I = \{ 1,2,3,4 \} $$

La relazione R è "x è maggiore o uguale di y"

$$ R = \{ (4;3),(4;2),(4;1),(3;2),(3;1),(2;1) \} $$

E' una relazione antisimmetrica perché quando prendo una coppia di elementi x e y diversi tra loro, se un elemento x è maggiore o uguale di y, allora y non è maggiore di x.

Nota. Ad esempio, l'elemento 4 è maggiore di 3. $$ 4>3 $$ Viceversa, l'elemento 3 non è maggiore di 4 $$ 3<4 $$ Quindi, la relazione è antisimmetrica.

Se rappresento la relazione in un grafo tra ogni coppia di nodi diversi non ci sono archi in entrambi i versi.

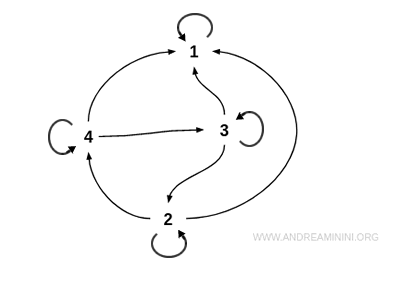
Gli unici archi bidirezionali sono tra un nodo e se stesso. Ad esempio, 3 è maggiore o uguale di 3, ecc.

Tuttavia, a differenza delle relazioni asimmetriche, nelle relazioni antisimmetriche questo dettaglio diventa irrilevante.

Ciò è dovuto al fatto che una delle condizioni fondamentali delle relazioni antisimmetriche è che gli elementi considerati debbano essere distinti tra loro.

Osservazioni

Alcune osservazioni sulle relazioni antisimmetriche

• Esistono relazioni che non sono né simmetriche, né antisimmetriche. Pertanto, se una relazione non è antisimmetrica, non è detto che sia simmetrica e viceversa.

  Esempio. Considero l'insieme $$ I = \{ -2,2,3,9,15 \} $$ e la relazione R "x è divisore proprio di y". $$ R = \{ (-2;2), (2;-2), (3;9), (3;15) \} $$ La relazione R non è antisimmetrica nell'insieme I perché tra gli elementi 2 e -2 c'è una relazione simmetrica. D'altra parte la relazione R non è nemmeno simmetrica nell'insieme I perché tra gli elementi 3 e 9 c'è una relazione antisimmetrica. Quindi, la relazione R non è né simmetrica, né antisimmetrica. Nel grafo della relazione R si nota un collegamento biunivoco tra due nodi (2 e -2) ma non tra ogni coppia di nodi.
  

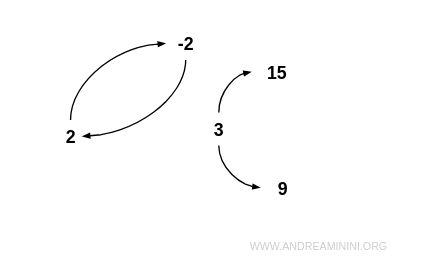
E così via.