La relazione simmetrica
Cosa sono le relazioni simmetriche
Una relazione è simmetrica per quando ogni elemento a in relazione con b, anche l'elemento b è in relazione con a. $$ \forall a,b \in X \ , \ aRb \Rightarrow bRa $$
Sono dette "simmetriche" perché generano una simmetria nella loro rappresentazione.
Ad esempio, se X è fratello di Y allora Y è fratello di X.
Le relazioni simmetriche sono un sottoinsieme delle relazioni definite in un insieme.
Nota. Una relazione simmetrica è detta relazione di equivalenza se è anche transitiva e riflessiva.
Un esempio pratico
Considero questo insieme
$$ A = \{ -1,-2,-3, 1, 2, 3 \} $$
La relazione R collega ogni numero nell'insieme con il suo numero opposto.
$$ R = \{ (-1;1),(-2;2),(-3;3),(1;-1),(2;-2),(3;-3) \} $$
La relazione è un sottoinsieme del prodotto cartesiano AxA
Rappresento la relazione in una tabella a doppia entrata.
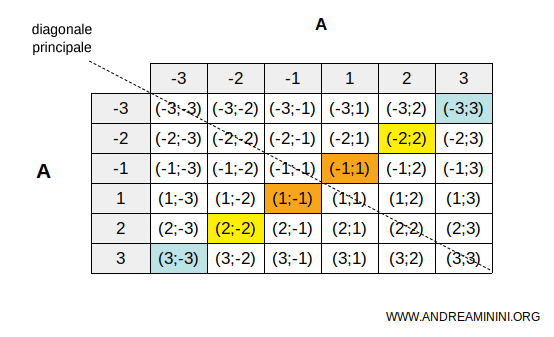
Nella tabella si manifesta una simmetria rispetto alla diagonale principale.
Per ogni casella che soddisfa la relazione (casella colorata) anche la relativa casella antisimmetrica soddisfa la relazione (stesso colore).
Ad esempio, -2 è il numero opposto di 2 ma anche 2 è il numero opposto di -2.
La simmetria si manifesta se rappresento la relazione in un diagramma cartesiano.
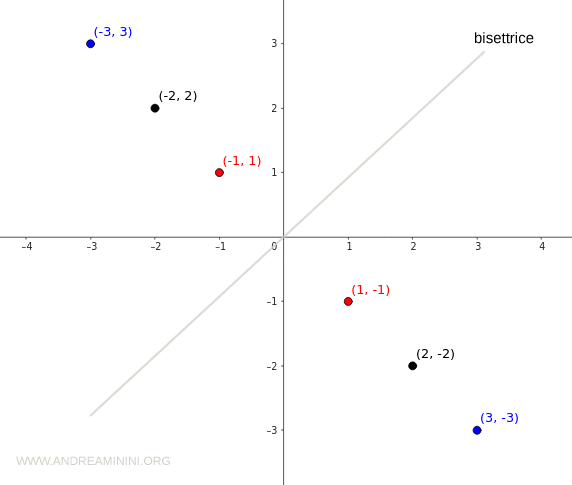
In questo caso la simmetria è rispetto alla bisettrice del diagramma.
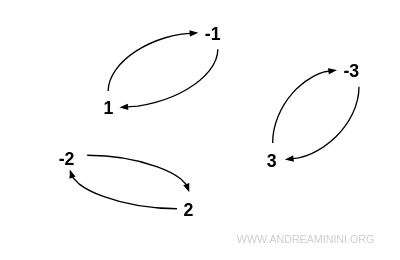
Nota. Nella rappresentazione di una relazione simmetrica tramite un grafo, invece, per ogni arco che collega un elemento a un altro, c'è un altro arco nel verso opposto.
Altri esempi
- La relazione "x è perpendicolare a y" è simmetrica perché se una retta x forma un angolo di 90° con un'altra retta y, allora anche la retta y forma un angolo di 90° con la retta x.
Osservazioni
Alcune osservazioni sulle relazioni simmetriche
- Se una relazione non è simmetrica, non è detto che sia anche asimmetrica. Esistono anche relazioni che non sono né simmetriche, né asimmetriche.
- La simmetria non è l'opposto dell'antisimmetria. Esistono relazioni né simmetriche, né antisimmetriche.
E così via.
