La relazione antiriflessiva

Cosa sono le relazioni antiriflessive

Una relazione definita in un insieme I è antiriflessiva se nessun elemento dell'insieme è in relazione con se stesso. $$\forall \ a \in I \ , \ a \require{cancel} \cancel{R} a$$

Nelle relazioni antiriflessive nessun elemento è collegato con se stesso.

Ad esempio, la relazione A è madre di B è antiriflessiva perché nessuna A è madre di se stessa.

Le relazioni antiriflessive sono un sottoinsieme delle relazioni definite in un insieme.

Un esempio pratico

Considero l'insieme finito I

$$I = \{ 2,4,3,9,16 \}$$

La relazione R collega gli elementi dell'insieme I con la loro radice quadrata ossia "x e la radice quadrata di y"

$$R = \{ (4;2),(16;4), (9;3) \}$$

La relazione è antiriflessiva perché nessun elemento dell'insieme I è la radice quadrata di se stesso.

Nota. Ad esempio, 2 non è la radice quadrata di se stesso. $$2 \ne \sqrt{2}$$ Lo stesso si può dire per tutti gli altri elementi dell'insieme I. Nella rappresentazione tramite un grafo le relazioni antiriflessive non presentano cappi, nessun nodo è collegato con se stesso.

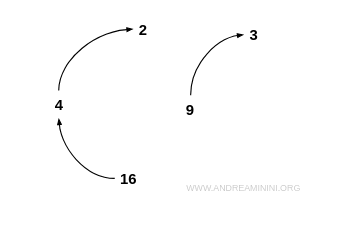
Osservazioni

Alcune osservazioni sulle relazioni antiriflessive

• Esistono relazioni che non sono né riflessive, né antiriflessive. Quindi, se una relazione non è antiriflessiva, non è detto che sia riflessiva e viceversa.

  Esempio. Considero l'insieme $$I = \{1,2,3,4,9,16 \}$$ e la relazione R in cui "x è la radice quadrata di y". La relazione R non è riflessiva perché non tutti gli elementi sono in relazione con se stessi. Ad esempio 2 non è la radice quadrata di 2. $$2 \ne \sqrt{2}$$ Tuttavia, la relazione non è nemmeno antiriflessiva perché in un singolo caso è riflessiva. Ad esempio 1 è la radice quadrata di 1. $$1 = \sqrt{1}$$ Nel grafo di questa relazione c'è un cappio. Quindi, non può essere antiriflessiva. Non essendoci cappi in tutti i nodi non è nemmeno riflessiva.
  

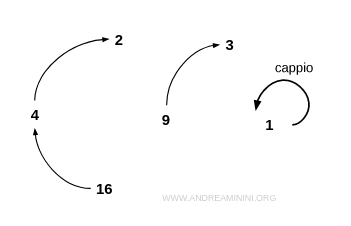
E così via.