Le relazioni definite in un insieme

Una relazione è definita in un insieme se associa gli elementi dell'insieme A con gli elementi dell'insieme A stesso.

In questo caso l'insieme di partenza e l'insieme di arrivo coincidono nello stesso insieme.

Questa relazione è definita nel prodotto cartesiano AxA.

Un esempio pratico

Considero l'insieme finito A

$$ A = \{ 2,3,4,5,6,7,8,9 \} $$

Il prodotto cartesiano dell'insieme per se stesso AxA è il seguente

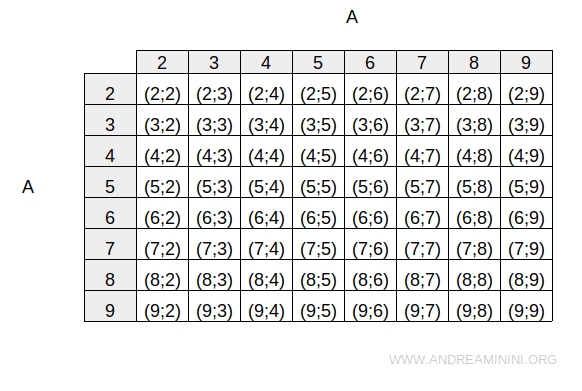
La relazione R definita nell'insieme A collega ogni elemento con i suoi multipli

$$ R = \{ (2;2) , (2;4),(2;6),(2;8),(3;3),(3;6),(3;9)\\ \ \ \ \ \ \ \ \ \ \ \ \ (4;4) , (4;8),(5;5),(6;6),(7;7),(8;8),(9;9) \} $$

La relazione genera un sottoinsieme del prodotto cartesiano AxA

Questa è la rappresentazione della relazione tramite una tabella a doppia entrata

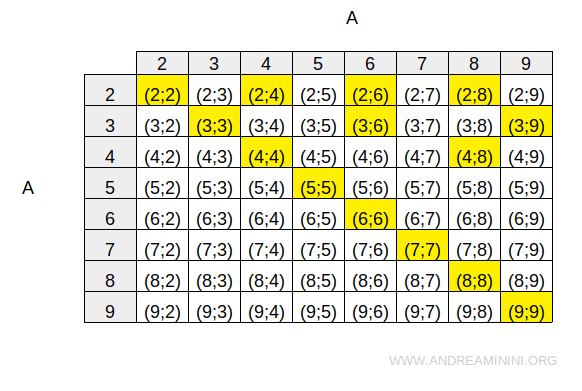
La rappresentazione sagittale della relazione definita in A è la seguente

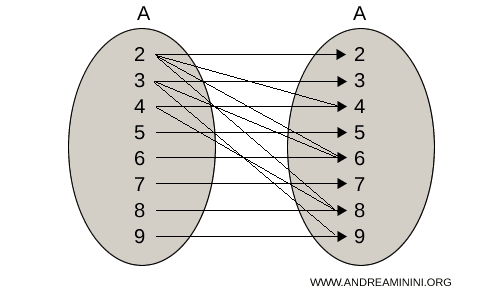
In questo caso l'insieme A è sia l'insieme di partenza che di destinazione.

La rappresentazione della relazione in un diagramma cartesiano è la seguente

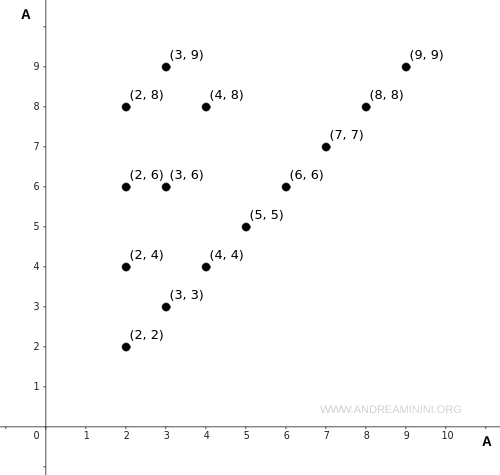
In questo caso l'insieme A appare sia sull'asse delle ascisse (orizzontale) che sull'asse delle ordinate (verticale).

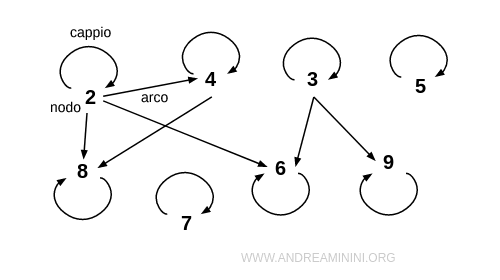
Nota. Le relazioni definite in un insieme posso rappresentarle molto più semplicemente usando un grafo. Basta scrivere ogni elemento dell'insieme A come un nodo, senza alcuna linea chiusa che li racchiuda, e collegare gli elementi tra loro tramite una freccia detta arco. Gli elementi in relazione con se stessi, ad esempio (2;2), formano un arco particolare detto cappio. Nel caso delle relazioni definite in un insieme la rappresentazione tramite i grafi è decisamente più leggibile, sintetica e chiara.

Tipi di relazioni definite in un insieme

Esistono diversi tipi di relazioni definite in un insieme

• Relazione riflessiva
  Una relazione R definita nell'insieme A è riflessiva se ogni elemento a∈A è in relazione con se stesso $$ \forall \ a \in A \Rightarrow \ aRa $$
• Relazione antiriflessiva
  Una relazione R definita nell'insieme A è antiriflessiva se nessun elemento a∈A è in relazione con se stesso $$ \forall \ a \ \in A \ \Rightarrow a \require{cancel} \cancel{R} a $$
• Relazione simmetrica
  Una relazione R definita nell'insieme A è simmetrica se, dati due elementi a,b∈A, per ogni elemento a in relazione con b anche l'elemento b è in relazione con a. $$ aRb \ \Leftrightarrow \ bRa $$
• Relazione asimmetrica
  Una relazione R definita nell'insieme A è asimmetrica se, dati due elementi a,b∈A, per ogni elemento a in relazione con b, b non è in relazione con a. $$ aRb \ \ \Rightarrow b \require{cancel} \cancel{R} a $$
• Relazione antisimmetrica
  Una relazione R definita nell'insieme A è antisimmetrica se, dati due elementi a,b∈A diversi tra loro (a≠b), per ogni elemento a in relazione con b, b non è in relazione con a. $$ aRb \ , \ a \ne b \ \Rightarrow b \require{cancel} \cancel{R} a $$

  Qual è la differenza tra asimmetrica e antisimmetrica? Una relazione antisimmetrica permette che due elementi siano in relazione reciproca solo se sono identici. In altre parole, se aRb e bRa, allora a deve essere uguale a b. $$ aRb \ , \ a \ne b \ \Rightarrow b \require{cancel} \cancel{R} a $$ D'altra parte, in una relazione asimmetrica, se un elemento è in relazione con un altro, l'altro non può essere in relazione con il primo, indipendentemente dal fatto che siano uguali o diversi. $$ aRb \ \ \Rightarrow b \require{cancel} \cancel{R} a $$ Quindi, nella relazione asimmetrica, non è permessa alcuna relazione reciproca, nemmeno tra elementi identici.

• Relazione transitiva
  Una relazione R definita nell'insieme A è transitiva se, dati tre elementi a,b,c∈A, se a è in relazione con b e b è in relazione con c, allora a è in relazione con c. $$ aRb \ , \ bRc \ \Rightarrow \ aRc $$

E così via.