I semigruppi
Cos'è un semigruppo
Un semigruppo (semigroup) è una struttura algebrica (S,*) composta da un insieme S e da una operazione binaria interna S×S→S, detta operazione di composizione, che soddisfa la proprietà associativa. $$ (a*b)*c=a*(b*c) \ \ \ \forall \ a,b,c \ \in S $$
E' anche detto pseudogruppo.
In un semigruppo non è necessario che esista un elemento neutro, né un elemento inverso.
Se il semigruppo è dotato anche di un elemento neutro, si parla di monoide.
Esempio
Prendo come esempio l'insieme dei numeri naturali N e l'operazione di addizione +.
$$ (N,+) $$
Si tratta di un gruppoide perché la struttura algebrica è composta da una operazione binaria interna.
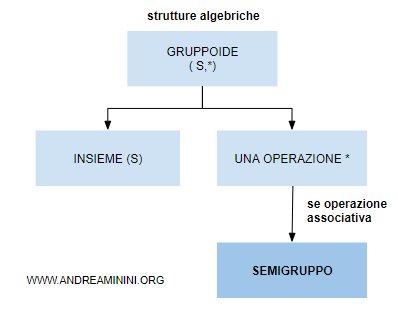
Inoltre, è anche un semigruppo perché l'operazione è associativa.
Dati tre numeri naturali qualsiasi a,b,c l'addizione rispetta la proprietà associativa.
$$ a+(b+c) = (a+b)+c $$
Se a=2, b=3, c=4
$$ 2+(3+4) = (2+3)+4 = 9 $$
E così via.
