Piano
Il piano è un ente fondamentale della geometria caratterizzato da due dimensioni (lunghezza e larghezza).
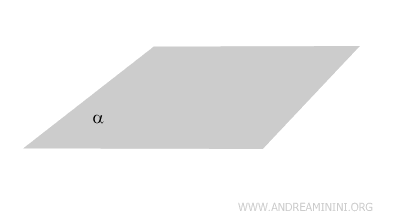
Un piano si estende all'infinito in tutte le direzioni e non ha spessore, né bordi.
In genere è indicato da una lettera dell'alfabeto greco (es. α, β, γ, δ, ecc.).
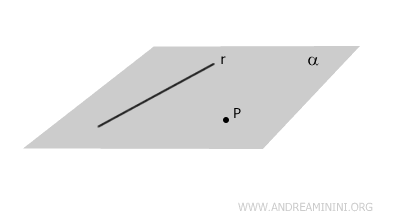
Quando una retta o un punto si trovano su un piano, si dice che appartengono al piano.
Ad esempio, la retta r appartiene al piano alfa.
Come si determina il piano?
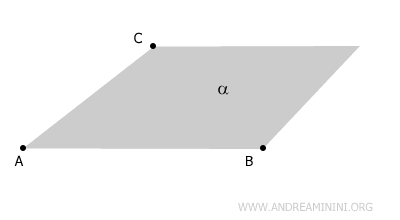
Un piano è determinato da tre punti non allineati (A, B,C) perché in tre punti non allineati passa uno e un solo piano α.
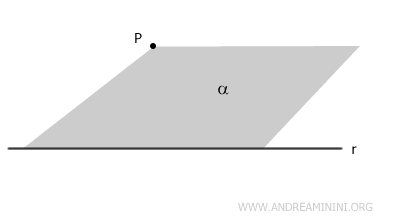
In alternativa, un piano può essere determinato anche da una retta e un punto non appartenente alla retta.
Per una retta r e un punto P non appartenente alla retta r passa uno e un solo piano α.
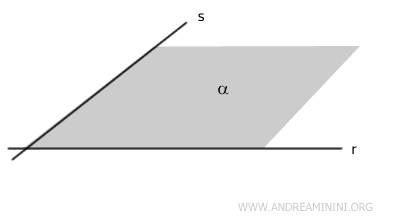
Infine, un piano può essere determinato anche da due rette incidenti.
Tra due rette incidenti r e s passa uno e un solo piano α.
Il semipiano
Il semipiano è una parte del piano divisa da una retta.
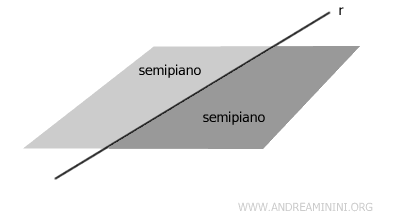
In altre parole, quando si traccia una retta su un piano, questa divide il piano in due parti distinte, ciascuna delle quali è un semipiano.
Piano incidenti e paralleli
In base alla loro posizione nello spazio, due piani distinti sono detti incidenti o paralleli.
- Piani incidenti
Due piani sono incidenti se hanno in comune una e sola retta.
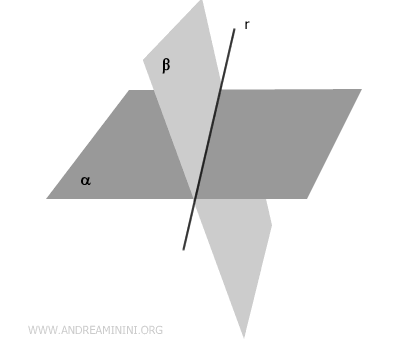
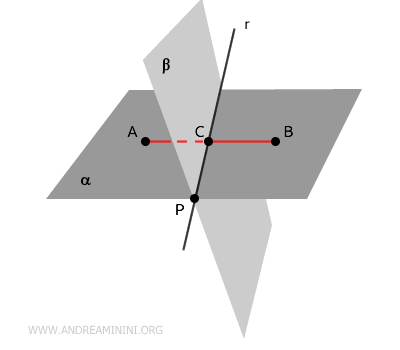
Teorema. Due piani distinti $ \alpha $ e $ \beta $ che si intersecano in un punto $ P \in \alpha \cap \beta $ hanno in comune una retta $ r $ che passa per quel punto. $$ \exists \ r \ | \ P \in r, r \in \alpha \cap \beta $$
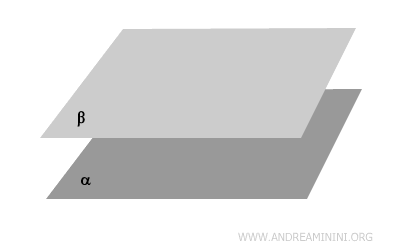
- Piani paralleli
Due piani sono paralleli se non hanno punti in comune (piani paralleli non coincidenti) oppure hanno tutti i punti in comune (piani coincidenti).
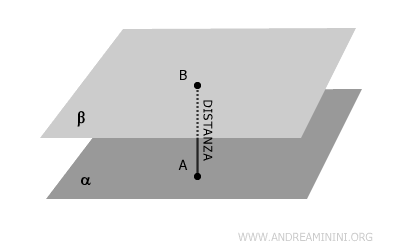
La distanza tra due piani paralleli è data dalla lunghezza del segmento che collega due punti, uno per ogni piano, ed è perpendicolare ad entrambi i piani.
La relazione di parallelismo tra piani gode della proprietà riflessiva, simmetrica e transitiva.
- Proprietà riflessiva
Ogni piano è parallelo a se stesso $$ \alpha || \alpha $$ - Proprietà simmetrica
Se il piano α è parallelo al piano β, allora il piano β è parallelo al piano α $$ \alpha || \beta \Leftrightarrow \beta || \alpha $$ - Proprietà transitiva
Se il piano α è parallelo al piano β e il piano β è parallelo al piano γ, allora il piano α è parallelo al piano γ $$ \alpha || \beta \ , \ \beta || \gamma \Rightarrow \alpha || \gamma $$
La posizione di una retta nel piano
Una retta sul piano può essere
- Retta complanare (o giacente sul piano)
La retta appartiene al piano. Tutti i punti della retta appartengono anche al piano r⋂α=r.
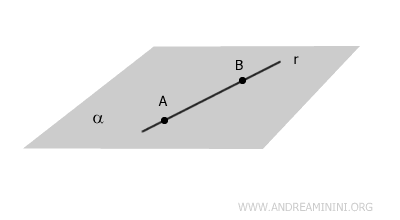
- Retta incidente
La retta e il piano hanno in comune solo un punto r⋂α={P}. Una retta incidente al piano può essere perpendicolare o obliqua al piano.
- Retta perpendicolare a un piano
se la retta è perpendicolare a ogni retta del piano che passa per il punto di incidenza (detto piede della perpendicolare).
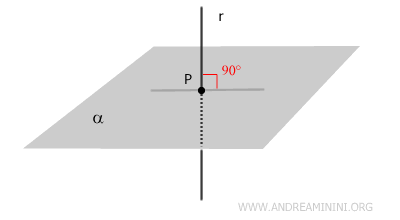
- Retta obliqua
se la retta non è perpendicolare al piano.
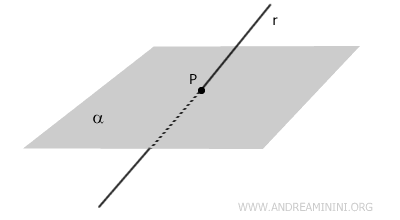
- Retta perpendicolare a un piano
- Retta parallela al piano
La retta non ha punti in comune con il piano r⋂α=Ø.
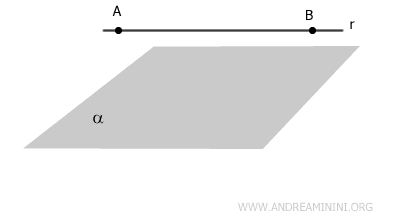
Se una retta \( r \) è parallela a un piano \( \alpha \), allora ogni altro piano \( \beta \) che contiene \( r \) e non è parallelo a \( \alpha \) interseca \( \alpha \) lungo una retta \( s \), parallela a \( r \).
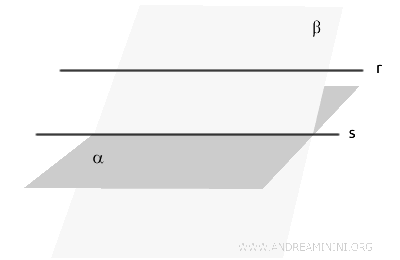
Questo accade perché le rette \( r \) e \( s \), essendo complanari, appartengono entrambe al piano \( \beta \) e non si incontrano mai.
E così via.
