Segmenti commensurabili e incommensurabili
Due segmenti sono commensurabili se il loro rapporto è un numero razionale \( \frac{a}{b} \), altrimenti sono incommensurabili.
Quando due segmenti sono commensurabili, possono essere suddivisi in un numero intero di parti uguali utilizzando un segmento comune come unità di misura.
Segmenti commensurabili
Due segmenti si dicono commensurabili se esiste un'unità di misura comune (un segmento di riferimento) tale che le lunghezze di entrambi i segmenti possano essere espresse come multipli interi di questa unità.
In poche parole... significa che il rapporto tra le loro lunghezze è un numero razionale \( \frac{a}{b} \) dove $ a $ e $ b $ sono due numeri interi.
Esempio
Considero due segmenti di lunghezza \(3\) cm e \(4\) cm.
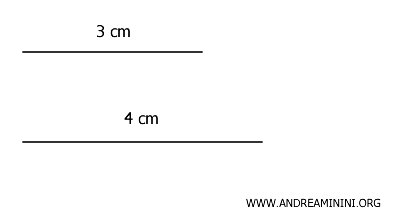
Poiché il loro rapporto è \(3/4\), che è un numero razionale, i segmenti sono commensurabili.
Questo significa che posso dividere entrambi i segmenti in un numero intero di parti tramite un segmento in comune.
Per trovare il segmento in comune, basta calcolare il massimo comune divisore (MCD) delle due misure.
$$ MCD(3, 4) = 1 $$
In questo caso il massimo comune divisore è 1, questo significa che posso suddividere i due segmenti da 3 cm e 4 cm con un segmento da 1 cm.
Dividendo entrambi i segmenti in unità da \(1\) cm, posso esprimere le loro lunghezze come \(3\) e \(4\) unità.
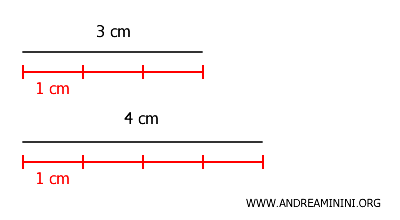
Segmenti incommensurabili
Due segmenti sono incommensurabili se non esiste un'unità di misura comune per esprimere le loro lunghezze come multipli interi.
Questo accade quando il rapporto tra le lunghezze dei segmenti è un numero irrazionale, ovvero non razionale.
Esempio
Un classico esempio geometrico è il lato e la diagonale di un quadrato.
Se il lato del quadrato misura \(1\) cm, in base al teorema di Pitagora la diagonale misura \( \sqrt{2} \) cm.
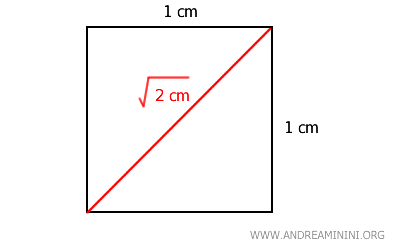
Il rapporto tra il lato del quadrato \( 1 \) e la diagonale \( \sqrt{2} \) non può essere espresso come un numero razionale $ \frac{a}{b} $, dove $ a $ e $ b $ sono numeri interi, perché \( \sqrt{2} \) è un numero irrazionale.
Pertanto, i due segmenti sono incommensurabili.
Nota. Questo esempio mise in crisi la scuola pitagorica perché contraddiceva la loro convinzione che tutti i rapporti fossero esprimibili come numeri razionali. Questa scoperta segnò un evento cruciale nella storia della matematica, portando alla scoperta dei numeri irrazionali. Secondo la tradizione, la scuola pitagorica voleva mantenere segreta la scoperta dell'irrazionalità, considerandola pericolosa per la loro visione del mondo basata sull'armonia e sulla razionalità dei numeri. Si racconta che chi rivelò questa verità, il discepolo Ippaso di Metaponto, fu severamente punito dai pitagorici, in alcuni racconti addirittura condannato a morte o gettato in mare.
E così via.
