La scomposizione di un vettore

La scomposizione di un vettore è la somma delle componenti del vettore v_x, v_y, v_z sugli assi cartesiani $$ \vec{v} = \vec{v_x} + \vec{v_y} + \vec{v_z} $$ che posso riscrivere come combinazione lineare dei versori u_x, u_y, u_z $$ \vec{v} = \alpha_1 \vec{u_x} + \alpha_2 \vec{u_y} + \alpha_3 \vec{u_z} $$

Dove i versori u_x, u_y, u_z sono i vettori unitari delle tre direzioni del sistema di riferimento (x,y,z).

Gli scalari α₁, α₂, α₃ sono invece dei numeri opportunamente scelti.

Cosa sono le componenti del vettore? Le componenti del vettore sono le proiezioni del vettore stesso sugli assi cartesiani. Ecco un esempio di componenti v_x e v_y di un vettore v sul piano cartesiano a due dimensioni (x,y).

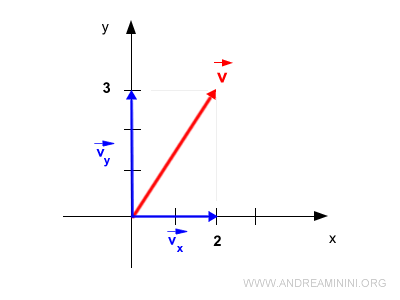
Anche le componenti del vettore sono a loro volta delle grandezze vettoriali. Non sono scalari.

Un esempio pratico

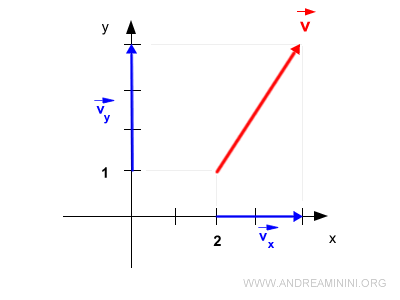
Prendo in considerazione il vettore v=(2,3)^T nello spazio a due dimensioni.

$$ \vec{v} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

Ecco la sua rappresentazione grafica

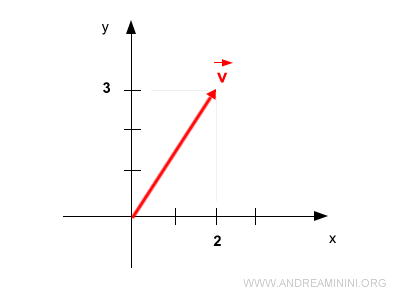
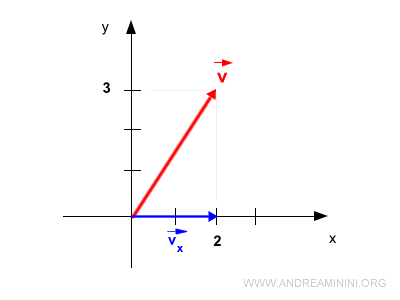
Proietto il vettore v sull'asse x delle ascisse e ottengo la sua componente v_x.

Dove anche v_x è una grandezza vettoriale.

Ora proietto il vettore v sull'asse y delle ordinate e ottengo la sua componente v_y.

Anche v_y è una grandezza vettoriale.

Ho ottenuto le componenti del vettore in entrambe le direzioni dello spazio.

$$ \vec{v_x} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} $$

$$ \vec{v_y} = \begin{pmatrix} 0 \\ 3 \end{pmatrix} $$

La somma vettoriale delle componenti v_x e v_y è uguale al vettore v.

$$ \vec{v_x} + \vec{v_y} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 3 \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \vec{v} $$

Posso riscrivere le componenti del vettore v_x e v_y come prodotto del relativo versore per uno scalare.

$$ \vec{v_x} = x \cdot \vec{u_x} $$

$$ \vec{v_y} = y \cdot \vec{u_y} $$

Dove x e y sono le coordinate del vettore v ossia x=2 e y=3

$$ \vec{v_x} = 2 \cdot \vec{u_x} $$

$$ \vec{v_y} = 3 \cdot \vec{u_y} $$

I versori degli assi cartesiani sono le direzioni ortogonali u_x=(1,0)^T e u_y=(0,1)^T del sistema cartesiano

$$ \vec{v_x} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$

$$ \vec{v_y} = 3 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

Quindi, la somma delle componenti v_x+v_y posso scriverla come combinazione lineare dei versori u_x e u_y per gli scalari 2 e 3

$$ \vec{v_x} + \vec{v_y} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 3 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

E poiché la somma delle componenti è uguale al vettore v

$$ \vec{v} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 3 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

La combinazione lineare dei versori con gli scalari mi permette di ottenere il vettore v iniziale

$$ \vec{v} = \vec{v_x} + \vec{v_y} $$

$$ \vec{v} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 3 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

$$ \vec{v} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 3 \end{pmatrix} $$

$$ \vec{v} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

Nota. Il modulo delle componenti v_x e v_y posso scriverlo anche con le funzioni trigonometriche del seno e del coseno. $$ | \vec{v_x} | = r \cdot \sin \Phi $$ $$ | \vec{v_y} | = r \cdot \cos \Phi $$ Dove Φ è l'angolo del vettore rispetto all'asse delle ascisse mentre r è la lunghezza del raggio vettore ossia il modulo del vettore v.

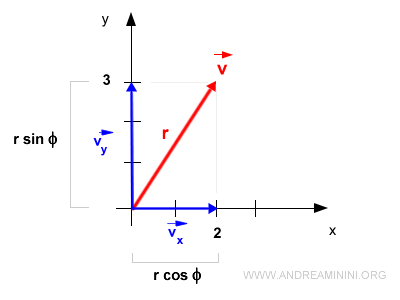
Il raggio vettore coincide con il raggio della circonferenza goniometrica. Per trovare la lunghezza r del raggio vettore basta applicare il teorema di Pitagora sui moduli (lunghezze) delle componenti v_x e v_y. $$ r = \sqrt{ |\vec{x}|^2 + |\vec{y}|^2 } $$ $$ r = \sqrt{ 2^2 + 3^2 } $$ $$ r = \sqrt{ 4 + 9 } $$ $$ r = \sqrt{ 13 } $$

Esempio 2

Se il vettore è applicato in un punto diverso dall'origine, la proiezione va calcolata sia all'estremo che all'origine del vettore.

E così via.