La dipendenza e l'indipendenza lineare dei vettori

Dati m vettori v₁, v₂, ... , v_m in uno spazio in uno spazio vettoriale V nel campo K, i vettori sono linearmente indipendenti tra loro se la combinazione lineare con m coefficienti scalari uguale al vettore nullo ha una sola soluzione banale. $$ a_1 \cdot \vec{v}_1 + a_2 \cdot \vec{v}_2+ \ ... \ + α_m \cdot \vec{v}_m = \vec{0} $$ Viceversa, se ha anche altre soluzioni non banali i vettori sono linearmente dipendenti tra loro.

Una combinazione lineare di vettori uguale al vettore nullo è detta banale quando tutti i coefficienti scalari sono nulli

$$ a_1 = a_2 = \ ... = \ a_m = 0 $$

Se almeno un coefficiente è diverso da zero, la soluzione della combinazione lineare non è banale.

Vettori linearmente indipendenti

In uno spazio vettoriale V sul campo K, i vettori v₁,...,v_m ∈ V sono linearmente indipendenti se nessuna combinazione lineare è uguale al vettore nullo, a parte la combinazione lineare banale. $$ α_1 \cdot \vec{v}_1 + ... + α_m \cdot \vec{v}_m = \vec{0} \ \ \ \ \ \ α \in K $$

Cos'è una combinazione lineare banale?

E' una combinazione lineare tra un vettore e una sequenza di zeri { a₁=0, ... , a_m=0 }.

Perché la combinazione lineare banale è esclusa?

La combinazione lineare banale non viene considerata, perché qualsiasi combinazione lineare di vettori con coefficienti nulli è uguale a un vettore nullo.

$$ 0 \cdot v_1 + ... + 0 \cdot v_m = 0 $$

Quindi la soluzione banale c'è sempre e non può dirmi nulla sulla dipendenza o indipendenza lineare dei vettori.

Vettori linearmente dipendenti

In uno spazio vettoriale V sul campo K, i vettori v₁,...,v_m ∈ V sono linearmente dipendenti se esiste una o più combinazioni lineari uguale al vettore nullo, oltre la combinazione lineare banale. $$ α_1 \cdot \vec{v}_1 + ... + α_m \cdot \vec{v}_m = \vec{0} \ \ \ \ \ \ α \in K $$

La soluzione banale viene esclusa perché non permette di distinguere tra la dipendenza e l'indipendenza lineare dei vettori.

Im questo caso, nella combinazione lineare c'è almeno un coefficiente scalare non nullo.

Ne consegue questo teorema

I vettori v₁,...,v_m sono linearmente dipendenti se almeno uno di essi ( es. v₁ ) si può scrivere come combinazione lineare dei vettori rimanenti.

$$ v_1 = β_2 \cdot v_2 + ... + β_m \cdot v_m $$ $$ con \: \: β_2 , ... , β_m \in R $$

Il teorema non dice però quale vettore si può scrivere come combinazione degli altri, afferma soltanto che esiste se i vettori sono linearmente dipendenti.

Potrebbere essere uno qualsiasi dei vettori v₁,...,v_m e non necessariamente v₁.

Interpretazione geometrica

Nello spazio R² due vettori sono linearmente dipendenti se sono paralleli o coincidenti, ossia si trovano sulla stessa retta e hanno la stessa direzione.

Nello spazio R³ tre vettori sono linearmente dipendenti se appartengono allo stesso piano.

Nota. Queste considerazioni geometriche le posso fare solo nel caso degli spazi vettoriali R² o R³. Non posso farle per spazi vettoriali di dimensioni superiori come R^4, R⁵, ecc.

Un esempio pratico

Esempio 1

Considero due vettori nello spazio vettoriale V=R² nel campo dei numeri reali K=R

$$ \vec{v}_1 = \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

$$ \vec{v}_2 = \begin{pmatrix} 2 \\ 5 \end{pmatrix} $$

La combinazione lineare è la seguente

$$ a_1 \cdot \vec{v}_1 + a_2 \cdot \vec{v}_2 = \vec{0} $$

$$ a_1 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} + a_2 \cdot \begin{pmatrix} 2 \\ 5 \end{pmatrix} = \vec{0} $$

Il vettore nullo è un vettore composto da due zeri.

$$ \begin{pmatrix} 3a_1 \\ a_1 \end{pmatrix} + \begin{pmatrix} 2a_2 \\ 5a_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

Riscrivo l'equazione vettoriale come sistema di equazioni

$$ \begin{cases} 3a_1 + 2a_2 = 0 \\ \\ a_1 + 5a_2 = 0 \end{cases} $$

Poi risolvo il sistema con il metodo della sostituzione mettendo in evidenza a₁ nella seconda equazione.

$$ \begin{cases} 3a_1 + 2a_2 = 0 \\ \\ a_1 = - 5a_2 \end{cases} $$

Nota. Qualsiasi altro metodo per risolvere il sistema va bene lo stesso. Ad esempio, il metodo di Cramer.

Poi sostituisco a₁ nella prima equazione e ottengo il valore di a₂=0.

$$ \begin{cases} 3(-5a_2) + 2a_2 = 0 \\ \\ a_1 = - 5a_2 \end{cases} $$

$$ \begin{cases}-15a_2 + 2a_2 = 0 \\ \\ a_1 = - 5a_2 \end{cases} $$

$$ \begin{cases}-13a_2 = 0 \\ \\ a_1 = - 5a_2 \end{cases} $$

$$ \begin{cases} a_2 = 0 \\ \\ a_1 = - 5a_2 \end{cases} $$

Una volta noto a₂ lo sostituisco nella seconda equazione e ottengo il valore di a₁=0.

$$ \begin{cases} a_2 = 0 \\ \\ a_1 = - 5(0) \end{cases} $$

$$ \begin{cases} a_2 = 0 \\ \\ a_1 = 0 \end{cases} $$

L'unica soluzione del sistema è il vettore nullo ossia a₁=0 e a₂=0.

Pertanto, i due vettori sono linearmente indipendenti.

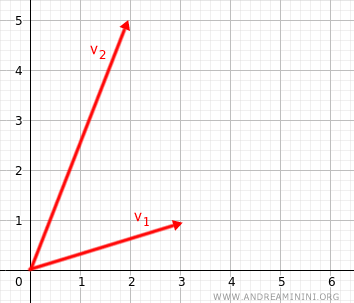
Nota. Nel caso di due vettori nello spazio a due dimensioni R², ossia sul piano, la dipendenza lineare si verifica solo quando i vettori sono paralleli. Pertanto, se i vettori sono linearmente indipendenti allora non sono vettori paralleli. Questa caratteristica però vale solo sul piano. Non vale negli spazi di dimensioni superiori.

Esempio 2

Considero tre vettori nello spazio vettoriale reale a due dimensioni V=R²

$$ \vec{v_1} = \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

$$ \vec{v_2} = \begin{pmatrix} 1 \\ 4 \end{pmatrix} $$

$$ \vec{v_3} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$

I tre vettori sono linearmente indipendenti se non esiste una combinazione lineare dei tre vettori con tre coefficienti scalari uguale al vettore nullo a parte la soluzione banale.

$$ a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + a_3 \cdot \vec{v_3} = \vec{0} $$

$$ a_1 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} + a_2 \cdot \begin{pmatrix} 1 \\ 4 \end{pmatrix} + a_3 \cdot \begin{pmatrix} 2 \\ 1 \end{pmatrix} = \vec{0} $$

$$ \begin{pmatrix} 3a_1 \\ a_1 \end{pmatrix} + \begin{pmatrix} a_2 \\ 4a_2 \end{pmatrix} + \begin{pmatrix} 2a_3 \\ a_3 \end{pmatrix} = \vec{0} $$

Per capire se sono linearmente indipendenti o dipendenti, trasformo l'equazione vettoriale in un sistema di equazioni.

$$ \begin{cases} 3a_1+a_2+2a_3=0 \\ a_1+4a_2 +a_3 = 0 \end{cases} $$

Poi verifico se esiste una soluzione non banale, ossia diversa dal vettore nullo dei coefficienti.

In questo caso è però inutile cercarla perché il sistema ha 3 variabili e 2 equazioni.

Quindi, per il teorema di Rouché-Capelli il sistema lineare ha infinite soluzioni oltre al vettore nullo (soluzione banale).

Pertanto, i tre vettori sono linearmente dipendenti.

Questo vuol dire che possono ottenere uno dei tre vettori come combinazione lineare degli altri due.

Esempio 3

In uno spazio vettoriale V=R³ con campo K=R ho due vettori:

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} $$ $$ v_2 = \begin{pmatrix} 3 \\ 2 \\ 3 \end{pmatrix} $$

Devo verificare se sono linearmente dipendenti.

Secondo la definizione sono linearmente dipendenti se la loro combinazione lineare è uguale a zero, con i coefficienti α non tutti contemporaneamente uguali a zero.

$$ α_1 \cdot v_1 + α_2 \cdot v_2 = 0 $$ $$ α_1 \cdot \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + α_2 \cdot \begin{pmatrix} 3 \\ 2 \\ 3 \end{pmatrix} = 0 $$ $$ ( α_1, 2α_1, -α_1 ) + ( 3α_2, 2α_2, 3α_2) = 0 $$

Posso rappresentare i due vettori come un sistema lineare con tre equazioni e due variabili incognite:

$$ \begin{cases} α_1 + 3α_2 = 0 \\ 2α_1 + 2α_2 = 0 \\ -α_1 + 3α_2 = 0 \end{cases} $$

Risolvo il sistema per verificare se ha una soluzione diversa da quella banale ( α₁=0 , α₂=0 )

$$ \begin{cases} α_1 + 3α_2 = 0 \\ 2α_1 + 2α_2 = 0 \\ α_1 = - 3α_2 \end{cases} $$

$$ \begin{cases} (- 3α_2) + 3α_2 = 0 \\ 2(- 3α_2) + 2α_2 = 0 \\ α_1 = - 3α_2 \end{cases} $$

$$ \begin{cases} 0 = 0 \\ -4α_2 = 0 \\ α_1 = - 3α_2 \end{cases} $$

Il sistema non ha soluzioni a parte quella banale ( α₁=0 , α₂=0 )

Quindi, i due vettori v₁ e v₂ non sono linearmente dipendenti.

Sono linearmente indipendenti.

Esempio 4

In uno spazio vettoriale V=R³ con campo K=R ho due vettori:

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} $$ $$ v_2 = \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} $$

Sono linearmente dipendenti se la loro combinazione lineare è uguale a zero, con i coefficienti α non tutti contemporaneamente uguali a zero.

$$ α_1 \cdot v_1 + α_2 \cdot v_2 = 0 $$ $$ α_1 \cdot \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + α_2 \cdot \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} = 0 $$ $$ ( α_1, 2α_1, -α_1 ) + ( 3α_2, 6α_2, 3α_2) = 0 $$

Rappresento i due vettori come un sistema lineare con tre equazioni e due variabili incognite:

$$ \begin{cases} α_1 + 3α_2 = 0 \\ 2α_1 + 6α_2 = 0 \\ -α_1 + 3α_2 = 0 \end{cases} $$

Poi risolvo il sistema

$$ \begin{cases} α_1 + 3α_2 = 0 \\ 2α_1 + 6α_2 = 0 \\ α_1 = - 3α_2 \end{cases} $$

$$ \begin{cases} (- 3α_2) + 3α_2 = 0 \\ 2(- 3α_2) + 6α_2 = 0 \\ α_1 = - 3α_2 \end{cases} $$

$$ \begin{cases} 0 = 0 \\ 0 = 0 \\ α_1 = - 3α_2 \end{cases} $$

Il sistema ha una soluzione diversa da quella banale.

Pertanto, i vettori v₁ e v₂ sono linearmente dipendenti.

Esempio 5

Dati 3 vettori nello spazio vettoriale V=R³

$$ v_1 = \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} $$

$$ v_3 = \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} $$

La loro combinazione lineare uguale al vettore nullo è

$$ a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + a_3 \cdot \vec{v_3} = \vec{0} $$

$$ a_1 \cdot \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} + a_2 \cdot \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} + a_3 \cdot \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$

$$ \begin{pmatrix} 3a_1 \\ a_1 \\ -2a_1 \end{pmatrix} + \begin{pmatrix} 2a_2 \\ -a_2 \\ 0 \end{pmatrix} + \begin{pmatrix} a_3 \\ -3a_3 \\ 2a_3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$

Trasformo l'equazione vettoriale in un sistema di equazioni cartesiane.

$$ \begin{cases} 3a_1 + 2a_2 + a_3 = 0 \\ a_1 - a_2 - 3a_3 = 0 \\ -2a_1 + 2a_3 = 0 \end{cases} $$

Cerco le soluzioni del sistema con il metodo della sostituzione.

Metto in evidenza la variabile a₁ nella terza equazione e la sostituisco nelle altre equazioni.

$$ \begin{cases} 3a_1 + 2a_2 + a_3 = 0 \\ a_1 - a_2 - 3a_3 = 0 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 3a_3 + 2a_2 + a_3 = 0 \\ a_3 - a_2 - 3a_3 = 0 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 4a_3 + 2a_2 = 0 \\ -a_2 - 2a_3 = 0 \\ a_1 = a_3 \end{cases} $$

Metto in evidenza la variabile a₂ nella seconda equazione e la sostituisco nelle altre equazioni.

$$ \begin{cases} 4a_3 + 2a_2 = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 4a_3 + 2(-2a_3) = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 4a_3 -4a_3 = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 0 = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

Quindi, il sistema ha infinite soluzioni perché a₃ può assumere qualsiasi valore e determinare a₁ e a₂.

Di conseguenza i vettori v₁, v₂, v₃ sono linearmente dipendenti tra loro.

Questo vuol dire che posso ottenere uno dei tre vettori con una combinazione lineare degli altri due vettori.

Nota. Guardando i tre vettori è evidente che il vettore v₃ lo posso ottenere con una combinazione lineare di v₂ e v₃ $$ \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} = 2 \cdot \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} - v_3 $$ $$ v_1 = 2v_2 - \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} $$

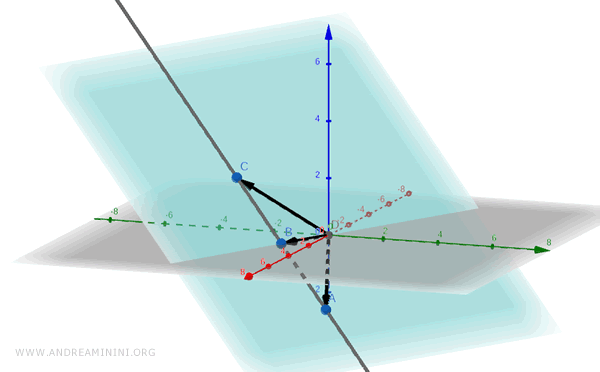
Dal punto di vista geometrico vuol dire che i tre vettori v₁, v₂, v₃ linearmente dipendenti si trovano in uno stesso piano nello spazio a tre dimensioni.

La dimostrazione

I vettori v₁,...,v_m sono linearmente dipendenti se la loro combinazione lineare è uguale al vettore nullo con coefficienti scalari α₁,...,α_m non tutti uguali a zero.

$$ α_1 \cdot \vec{v}_1 + ... + α_m \cdot \vec{v}_m = \vec{0} $$

Per ipotesi considero il coefficiente scalare α₁ diverso da zero

$$ a_1 \ne 0 $$

Metto in evidenza il vettore v₁ spostando tutti gli altri vettori a destra

$$ α_1 \cdot \vec{v}_1 = - α_2 \cdot \vec{v}_2 ... - α_m \cdot \vec{v}_m $$

Sapendo che α₁ è diverso da zero, divido entrambi i membri dell'equazione per α₁

$$ (\frac{1}{α_1}) \cdot α_1 \cdot \vec{v}_1 = (\frac{1}{α_1}) \cdot ( - α_2 \cdot \vec{v}_2 ... - α_m \cdot \vec{v}_m ) $$

$$ \vec{v}_1 = - \frac {α_2 } {α_1} \cdot \vec{v}_2 ... - \frac {α_m} {α_1} \cdot \vec{v}_m $$

Per semplicità scrivo i rapporti tra gli scalari con la lettera beta (β)

$$ b_2 = - \frac {α_2 } {α_1} \\ b_3 = - \frac {α_3 } {α_1} \\ \vdots \\ b_m = - \frac {α_m } {α_1} $$

E ottengo l'espressione che volevo dimostrare.

$$ \vec{v}_1 = β_2 \cdot \vec{v}_2 + ... + β_m \cdot \vec{v}_m $$

Nota. Dove i coefficienti beta sono i rapporti $$ β_2 = - \frac {α_2 } {α_1} $$ $$ ... $$ $$ β_m = - \frac {α_m } {α_1} $$

Ora dimostro il contrario, se un vettore v₁ è ottenuto dalla combinazione lineare dei restanti vettori

$$ \vec{v}_1 = β_2 \cdot \vec{v}_2 + ... + β_m \cdot \vec{v}_m $$

allora i vettori v₁,v₂,...,v_m sono linearmente dipendenti.

$$ - \vec{v}_1 + β_2 \cdot \vec{v}_2 + ... + β_m \cdot \vec{v}_m = \vec{0} $$

Se per ipotesi i coefficienti scalari α₂=0 , .... , α_m=0 sono nulli, allora anche i coefficienti β₂ ... β_m sono nulli.

$$ - \vec{v}_1 + 0 \cdot \vec{v}_2 + ... + 0 \cdot \vec{v}_m = \vec{0} $$

Ne consegue che la combinazione lineare si riduce a

$$ - \vec{v}_1= \vec{0} $$

Non si tratta di una combinazione lineare banale, perché il coefficiente del vettore v₁ è diverso da zero β=-1 per l'ipotesi iniziale.

Quindi la combinazione lineare non è banale.

Corollario 1

Se v₁,...,v_m sono vettori linearmente dipendenti, allora ogni suo sottoinsieme di vettori è linearmente dipendente.

Dimostrazione

Per ipotesi iniziale α₁=1.

Quindi, la seguente combinazione lineare non è banale e i vettori sono linearmente dipendenti.

$$ α_1 \cdot \vec{v}_1 + ... + α_m \cdot \vec{v}_m = 0 $$

Se α_m=0 posso eliminare l'ultimo termine della combinazione lineare.

$$ α_1 \cdot \vec{v}_1 + ... + α_{m-1} \cdot \vec{v}_{m-1} + 0 \cdot \vec{v}_m = 0 $$

$$ α_1 \cdot \vec{v}_1 + ... + α_{m-1} \cdot \vec{v}_{m-1} = 0 $$

Sapendo che α₁ è diverso da zero per l'ipotesi iniziale, anche quest'ultimo sottoinsieme della combinazione lineare non è banale.

Corollario 2

Se v₁,...,v_m sono vettori linearmente dipendenti, allora ogni insieme di vettori { v₁,...,v_m+k } che lo comprende è linearmente dipendente, ponendo a zero i coefficienti α_m=0,...,α_m+k=0.

Dimostrazione

$$ α_1 \cdot \vec{v}_1 + ... + α_m \cdot \vec{v}_m + ( α_{m+1} \cdot \vec{v}_{m+1} + ... + α_{m+k} \cdot \vec{v}_{m+k} ) = 0 $$

$$ con \: \: α_{m+1} = 0 \; , \; .... \; , \; α_{m+k} \: = \: 0 $$

$$ α_1 \cdot \vec{v}_1 + ... + α_m \cdot \vec{v}_m + ( 0 \cdot \vec{v}_{m+1} + ... + 0\cdot \vec{v}_{m+k} ) = 0 $$

$$ α_1 \cdot \vec{v}_1 + ... + α_m \cdot \vec{v}_m = 0 $$

Come calcolare la dipendenza lineare con il rango della matrice

Posso verificare la dipendenza e l'indipendenza lineare dei vettori numerici anche osservando il rango della matrice del sistema di equazioni.

Un insieme di n vettori numerici v₁, ... , v_n è linearmente indipendente se il rango per righe della matrice M_m,n(R) è uguale a n.
$$ r_k = n $$

Il rango per colonne di una matrice M(R) è il numero massimo di colonne indipendenti, se le colonne sono considerate come vettori numerici di n elementi.

• Se r_k=n le colonne sono linearmente indipendenti
• Se r_k<n le colonne sono linearmente dipendenti

Quando le colonne sono linearmente dipendenti (r_k<n) è comunque possibile cercare un sottoinsieme di vettori indipendenti tra i minori complementari non nulli della matrice

Sono indipendenti i vettori compresi in un minore complementare con determinante non nullo.

Nota. Lo stesso discorso si potrebbe fare usando le righe al posto delle colonne, se le righe sono considerate come vettori numerici. In una matrice M_m,n(R) il rango della matrice coincide con il rango per rango righe e con il rango per colonne.

Un esempio pratico

In uno spazio vettoriale V=R⁴ con campo K=R ho quattro vettori:

$$ v_1 = ( 1, 0, 1, 2 ) $$ $$ v_2 = ( 1, 3, 0, 0 ) $$ $$ v_3 = ( 1, -3, 2, 4 ) $$ $$ v_4 = ( 2, 3, 1, 2 ) $$

La combinazione lineare dei vettori è la seguente

$$ α_1 \cdot v_1 + α_2 \cdot v_2 + α_3 \cdot v_3 + α_4 \cdot v_4 $$

$$ α_1 \cdot ( 1, 0, 1, 2 ) + α_2 \cdot ( 1, 3, 0, 0 ) + α_3 \cdot ( 1, -3, 2, 4 ) + α_4 \cdot ( 2, 3, 1, 2 ) $$

Dispongo i vettori numerici in colonna formando una matrice quadrata 4x4

$$ M_{4,4} \begin{bmatrix} 1 & 0 & 1 & 2 \\ 1 & 3 & 0 & 0 \\ 1 & -3 & 2 & 4 \\ 2 & 3 & 1 & 2 \\ \end{bmatrix} $$

Poi calcolo il determinante di M_{4,4}.

$$ \bigtriangleup M = 0 $$

La matrice ha un determinante pari a zero. Quindi ha un rango r_k inferiore a 4.

Per trovare il rango della matrice M uso il teorema degli orlati.

Prendo un minore complementare di ordine 2 con determinante non nullo.

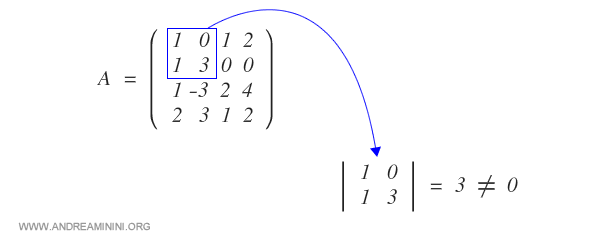
Questo mi fa capire che la matrice ha un rango uguale a 2 o superiore.

Per verificare se la matrice ha un rango pari a 3 verifico se almeno uno degli orlati ha determinante non nullo.

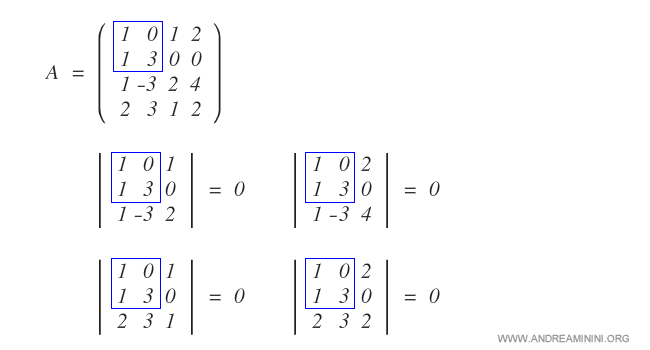
Gli orlati hanno tutti un determinante nullo.

Pertanto, secondo il teorema degli orlati, la matrice non ha un rango 3 o superiore.

La matrice ha un rango pari a 2.

Una volta calcolato il rango della matrice, posso subito capire la dipendenza o l'indipendenza dei vettori.

La matrice è composta da n=4 incognite (colonne) ma ha un rango r_k=2.

$$ r_k \ne n $$

Secondo il teorema:

1. Se r_k=n i vettori sono linearmente indipendenti.
2. Se r_k≠n i vettori sono linearmente dipendenti.

Quindi, i vettori v₁, v₂, v₃, v₄ sono linearmente dipendenti.

E per trovare i vettori indipendenti?

Basta selezionare a due a due i vettori nei minori complementari, quelli con minore complementare di ordine 2 con determinante non nullo sono tra loro vettori indipendenti.

Ad esempio, i vettori v₁ e v₂ sono vettori indipendenti tra loro perché sono compresi in un minore complementare con determinante non nullo.

In questo caso il rango della matrice (2) eguaglia il numero 2 delle incognite (colonne) del minore complementare.

Lo stesso calcolo si può fare per verificare il rapporto di indipendenza tra il vettore v₂ e v₃, v₃ e v₄, v₂ e v₄, v₁ e v₃, v₁ e v₄.

L'algoritmo di eliminazione di Gauss

Posso verificare la dipendenza lineare con il rango della matrice anche tramite l'algoritmo di eliminazione di Gauss-Jordan.

Secondo Gauss, il numero dei pivot eguaglia il rango della matrice.

Esempio

Nell'esercizio precedente i quattro vettori sono disposti in colonna in una matrice 4x4.

$$ M_{4,4} \begin{bmatrix} 1 & 1 & 1 & 2 \\ 0 & 3 & -3 & 3 \\ 1 & 0 & 2 & 1 \\ 2 & 0 & 4 & 2 \\ \end{bmatrix} $$

Poi trasformo la matrice in una matrice a gradini usando le regole di Gauss.

$$ M_{4,4} \begin{bmatrix} 1 & 0 & 2 & 1 \\ 0 & 1 & -1 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} $$

Nota. Per non appesantire ulteriormente la spiegazione, evito di scrivere tutti i passaggi della trasformazione della matrice in una matrice a gradini con l'algoritmo di Gauss-Jordan. Per vederli in dettaglio clicca qui.

La matrice ha due gradini ( pivot ), quindi ha rango pari a due ( r_k = 2 ).

Pertanto, i vettori v₁, v₂, v₃ e v₄ sono linearmente dipendenti perché r_k < n.

I due vettori v₁, v₂ dove si trovano i pivot sono linearmente indipendenti tra loro.

Nota. La matrice a gradini è utile soltanto per il calcolo del rango. Gli elementi dei vettori restano quelli originari ossia v₁ = ( 1, 1, 1, 2 ) , v₂ = ( 0, 3, -3, 3 ), v₃ = ( 1, 0, 2, 1 ) e v₄ = ( 2, 0, 4, 2 ).

Teoremi sull'indipendenza lineare dei vettori

• Se un insieme di vettori {v₁,v₂,...,v_n} sono vettori linearmente indipendenti, allora tutti i vettori sono diversi dal vettore nullo $$ \vec{v}_1 \ne \vec{0} \\ \vec{v}_2 \ne \vec{0} \\ \vdots \\ \vec{v}_n \ne \vec{0} $$

  Vedi dimostrazione.

• Dato uno spazio vettoriale V finitamente generato, se considero un insieme di generatori di V $$ \{ v_1, v_2, ..., v_n \} $$ e un insieme di vettori linearmente indipendenti appartenenti a V $$ \{ w_1, w_2, ..., w_p \} $$ allora $$ p \le n $$

  In pratica, il numero di vettori linearmente indipendenti di V è sempre inferiore o uguale al numero dei vettori in un insieme di generatori di V.
  
  Vedi dimostrazione

Osservazioni

Alcune osservazioni utili sulla dipendenza e indipendenza lineare dei vettori.

• Il vettore nullo è un vettore linearmente dipendente
  Secondo la definizione un vettore è linearmente indipendente se è uguale al vettore nullo solo quando tutti i coefficienti della combinazione lineare sono nulli (soluzione banale α=0). $$ \alpha \cdot \vec{v} = \vec{0} $$ Il vettore nullo è uguale al vettore nullo (a se stesso) anche quando il coefficiente scalare α della combinazione lineare è diverso da zero (α≠0). $$ \alpha \cdot \vec{0} = \vec{0} $$ Quindi, il vettore nullo è sempre un vettore linearmente dipendente.

E così via.