L'equazione vettoriale, parametrica e cartesiana del piano
Un piano è descritto da due vettori geometrici linearmente indipendenti in direzione distinte e da un punto passante per il piano.
$$ v_1 = \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} \:\:\: v_2 = \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$
$$ P_0 = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} $$
Se non indicassi il punto P0, i due vettori geometrici v1 e v2 individuerebbero tutti i piani paralleli ai vettori e non un piano in particolare.
Pertanto, ogni punto di un piano può essere descritto dalla seguente equazione vettoriale del piano.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \cdot \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$
Dall'equazione vettoriale è facile ottenere le equazioni parametriche del piano.
$$ \begin{cases} x = x_0 + t_1 \cdot l_1 + t_2 \cdot l_2 \\ y = y_0 + t_1 \cdot m_1 + t_2 \cdot m_2 \\ z = z_0 + t_1 \cdot n_1 + t_2 \cdot n_2 \end{cases} $$
Posso riscrivere le equazioni parametriche in questa forma.
$$ \begin{cases} x - x_0 = t_1 \cdot l_1 + t_2 \cdot l_2 \\ y - y_0 = t_1 \cdot m_1 + t_2 \cdot m_2 \\ z - z_0 = t_1 \cdot n_1 + t_2 \cdot n_2 \end{cases} $$
Ottengo così tre vettori P0P, v1 e v2 e posso disporli in colonna in una matrice quadrata.
$$ \begin{pmatrix} x - x_0 & l_1 & l_2 \\ y - y_0 & m_1 & m_2 \\ z - z_0 & n_1 & n_2 \end{pmatrix} $$
Calcolando il determinante della matrice ottengo l'equazione cartesiana del piano.
$$ det \begin{pmatrix} x - x_0 & l_1 & l_2 \\ y - y_0 & m_1 & m_2 \\ z - z_0 & n_1 & n_2 \end{pmatrix} = $$
$$ (x-x_0) \cdot det \begin{pmatrix} m_1 & m_2 \\ n_1 & n_2 \end{pmatrix} + (y-y_0) \cdot det \begin{pmatrix} l_1 & l_2 \\ n_1 & n_2 \end{pmatrix} + (z-z_0) \cdot det \begin{pmatrix} l_1 & l_2 \\ m_1 & m_2 \end{pmatrix} $$
Un esempio pratico
Ho due vettori direttori
$$ v_1 = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} \:\:\: v_2 = \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$
e un punto
$$ P = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} $$
Verifico se i due vettori sono linearmente indipendenti.
Il rango dei due vettori è uguale a due. Quindi sono linearmente indipendenti.
$$ r_k = \begin{pmatrix} 3 & 4 \\ 1 & 3 \\ 2 & 1 \end{pmatrix} = 2 $$
Nota. Se il rango eguaglia il numero dei vettori, i due vettori sono linearmente indipendenti.
A questo punto verifico se il punto P è un punto del piano.
Come verificare se un punto appartiene al piano
Se il punto P appartiene al piano esistono due parametri t1 e t2 che risolvono la seguente combinazione lineare e il relativo sistema lineare.
$$ \overrightarrow{OP} = \overrightarrow{OP_0} + t_1 v_1 + t_2 v_2 $$
Sostituisco i vettori direttori.
$$ \overrightarrow{OP} = \overrightarrow{OP_0} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$
Poi prendo come punto di riferimento P0 del piano uno dei due punti terminali dei vettori.
Ad esempio (3,1,2).
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_1\cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$
Infine, sostituisco alle coordinate (x,y,z) quelle del punto (10,5,5) e verifico se il sistema ha una soluzione.
$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_1\cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$
Il sistema ha una soluzione.
Per ottenere il punto (10,5,5) posso assegnare ai parametri i valori t1=1 e t2=1.
$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + 1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + 1 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$
$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 + 3 + 4 \\ 1 + 1 + 3 \\ 2 + 2 + 1 \end{pmatrix} $$
$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} $$
Pertanto l'equazione vettoriale del piano è la seguente:
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \cdot \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$
Una verifica alternativa. Per verificare l'esistenza di una soluzione del sistema, avrei potuto trasformare l'equazione vettoriale in tre vettori $$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$ $$ \begin{pmatrix} 10-3 \\ 5-1 \\ 5-2 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$ $$ \begin{pmatrix} 7 \\ 4 \\ 3 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$ Poi disporre in colonna i vettori dei coefficienti dell'equazione in una matrice. $$ \begin{pmatrix} 7 & 3 & 4 \\ 4 & 1 & 3 \\ 3 & 2 & 1 \end{pmatrix} $$ Se il rango della matrice è minore al numero dei vettori ossia è minore di tre allora i tre vettori sono linearmente dipendenti e il sistema ha una soluzione. In questo caso il rango della matrice è due (rk=2). Pertanto, il sistema ha una soluzione. $$ r_k = 2 < 3 $$ La spiegazione è molto semplice. I vettori v1(3,1,2) e v2(4,3,1) sono linearmente indipendenti. Per appartenere al piano, il primo vettore (7,1,3) deve essere linearmente dipendente da v1 e v2.
Una volta ottenuta l'equazione vettoriale posso calcolare facilmente l'equazione parametrica del piano.
E' sufficiente trasformarla in un sistema di equazioni.
$$ \begin{cases} x = 10 + t_1 \cdot 3 + t_2 \cdot 4 \\ y = 5 + t_1 \cdot 1 + t_2 \cdot 3 \\ z = 5 + t_1 \cdot 2 + t_2 \cdot 1 \end{cases} $$
$$ \begin{cases} x = 10 + 3t_1 + 4t_2 \\ y = 5 + t_1 + 3t_2 \\ z = 5 + 2t_1 + t_2 \end{cases} $$
Infine, per ottenere l'equazione cartesiana del piano trasformo l'equazione vettoriale in tre segmenti.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} - \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$
$$ \begin{pmatrix} x - 10 \\ y - 5 \\ z-5 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$
Poi metto i tre vettori in colonna dentro una matrice.
$$ \begin{pmatrix} x - 10 & 3 & 1 \\ y - 5 & 1 & 3 \\ z-5 & 2 & 1 \end{pmatrix} $$
Il determinante della matrice è l'equazione cartesiana del piano.
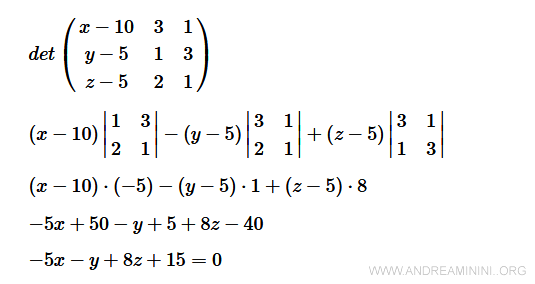
Ho così trovato anche l'equazione cartesiana del piano.
La rappresentazione grafica del piano in un diagramma a tre dimensioni è la seguente:
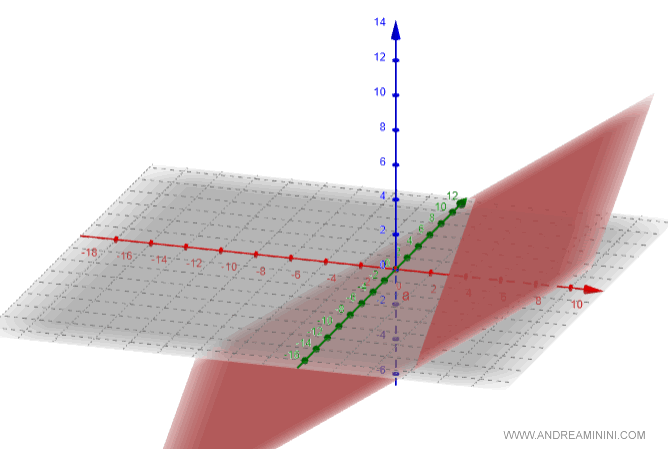
Come passare dall'equazione cartesiana all'equazione parametrica del piano
Provo a fare il processo inverso. Conosco l'equazione cartesiana del piano e voglio ottenere l'equazione parametrica.
L'equazione cartesiana del piano è
$$ ax + by + +cz + d = 0 $$
L'equazione vettoriale-parametrica del piano è la seguente:
$$ P = P_0 + t_1 v_1 + t_2 v_2 $$
I coefficienti a,b,c dell'equazione cartesiana determinano il vettore normale dell'equazione, ossia un vettore ortogonale al piano.
$$ n = \begin{pmatrix} a \\ b \\ c \end{pmatrix} $$
Se il vettore normale è ortogonale al piano, il vettore normale è ortogonale anche per qualsiasi vettore del piano.
Quindi, il vettore normale è ortogonale ai vettori direttori dell'equazione parametrica del piano.
Pertanto, il prodotto scalare tra il vettore normale e i vettori direttori è nullo.
$$ < n , v_2 > = 0 $$
$$ < n , v_1 > = 0 $$
Questa relazione mi consente di trovare due vettori linearmente indipendenti ortogonali al vettore normale e costruire l'equazione vettoriale/parametrica del piano.
Esempio
Ho la seguente equazione cartesiana
$$ -5x -y +8z + 15 = 0 $$
Il vettore normale dell'equazione è
$$ n = \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} $$
Il vettore normale è un vettore ortogonale al piano cartesiano.
E' quindi ortogonale a tutti i vettori non nulli presenti nel piano.
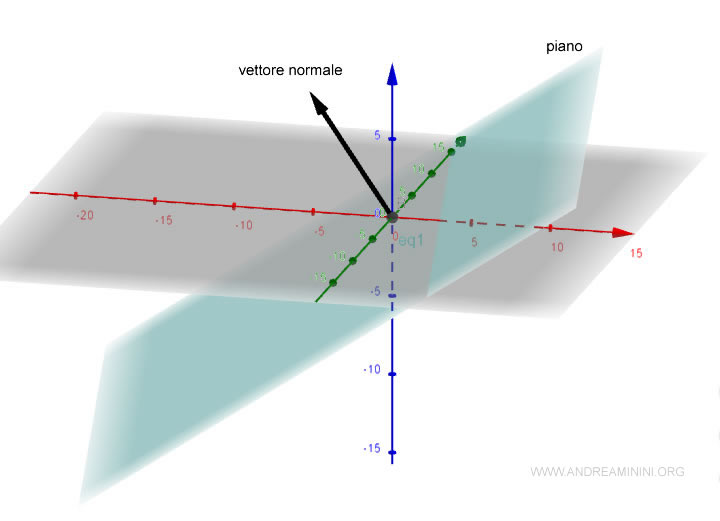
Ora devo cercare due vettori linearmente indipendenti che siano ortogonali al vettore normale.
Per trovarli metto a zero una coordinata del vettore normale, inverto le altre due e inverto il segno di una di queste ultime.
Ad esempio metto a zero la x del vettore normale.
$$ \begin{pmatrix} 0 \\ -1 \\ 8 \end{pmatrix} $$
Inverto le altre due
$$ \begin{pmatrix} 0 \\ 8 \\ -1 \end{pmatrix} $$
Poi cambio il segno a una di queste ultime.
Ho così trovato il primo vettore direttore dell'equazione del piano.
$$ v_1 = \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} $$
Con lo stesso metodo trovo anche il secondo vettore direttore.
Ad esempio, metto a zero la y.
$$ \begin{pmatrix} -5 \\ 0 \\ 8 \end{pmatrix} $$
Inverto le restanti coordinate.
$$ \begin{pmatrix} 8 \\ 0 \\ -5 \end{pmatrix} $$
Poi cambio il segno a una di queste ultime.
$$ v_2 = \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} $$
Ho trovato due vettori ortogonali al vettore normale.
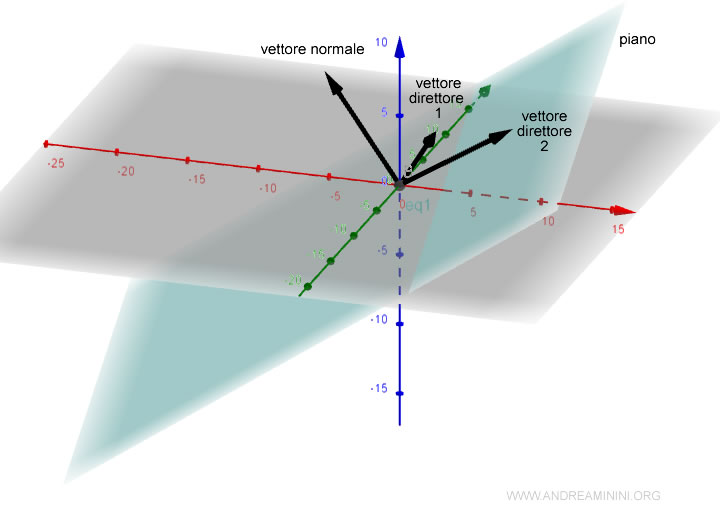
Verifico che siano vettori linearmente indipendenti.
$$ r_k \begin{pmatrix} 0 & 8 \\ 8 & 0 \\ 1 & 5 \end{pmatrix} = 2 $$
Il rango della matrice con i vettori in colonna è uguale a 2, ossia al numero dei vettori.
Quindi i due vettori sono linearmente indipendenti.
A questo punto verifico che siano anche ortogonali con il vettore normale.
$$ < n , v_1 > = < \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} , \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} > = 0 $$
$$ < n , v_2 > = < \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} , \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} > = 0 $$
Il prodotto scalare è nullo.
Quindi i due vettori v1 e v2 sono vettori ortogonali con il vettore normale.
Posso usarli come vettori direttori del piano.
Una volta verificata l'indipendenza lineare e l'ortogonalità, posso sostituire vettori direttori v1 e v2 nell'equazione vettoriale del piano.
$$ P = P_0 + t_1 v_1 + t_2 v_2 $$
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} + t_2 \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} $$
E' l'equazione parametrica del piano e di tutti i piani paralleli.
Per restringere l'equazione al solo piano che mi interessa, mi basta aggiungere un punto qualsiasi P0 del piano.
Ad esempio, assegno x=0 e z=0 all'equeazione cartesiana per determinare la coordinata della y.
$$ -5x -y +8z + 15 = 0 \\ -5(0) -y +8(0) + 15 = 0 \\ y =15$$
Ho così ottenuto un punto qualsiasi del piano P(x,y,z)=(0,15,0).
Lo sostituisco nell'equazione vettoriale al posto di P0.
Ho così trovato l'equazione vettoriale del piano.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 15 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} + t_2 \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} $$
Una volta trovata l'equazione vettoriale è facile passare all'equazione parametrica del piano.
Devo soltanto trasformare i vettori in un sistema di equazioni.
$$ \begin{cases} x = 8t_2 \\ y = 15 +8 t_1 \\ z = t_1 + 5t_2 \end{cases} $$
Come trovare l'equazione cartesiana dal vettore normale
Ho la seguente equazione cartesiana
$$ -5x -y +8z + 15 = 0 $$
Il vettore normale dell'equazione è
$$ n = \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} $$
Il vettore normale è un vettore ortogonale al piano cartesiano.
Individuo un punto qualsiasi del piano.
Metto a zero le coordinate y e z per calcolare il valore della x.
$$ -5x -y +8z + 15 = 0 $$
$$ -5x -(0) +8(0) + 15 = 0 $$
$$ x = 15 $$
Ho trovato un punto P1 del piano.
$$ P_1 = \begin{pmatrix} 15 \\ 0 \\ 0 \end{pmatrix} $$
Prendo in considerazione un punto generico del piano.
$$ P = \begin{pmatrix} x \\ y \\ z \end{pmatrix} $$
Calcolo il segmento tra i due punti.
$$ P_1P= \begin{pmatrix} x \\ y \\ z \end{pmatrix} - \begin{pmatrix} 15 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} x -15\\ y \\ z \end{pmatrix} $$
Ho così trovato un generico vettore v del piano.
So già che qualsiasi vettore del piano deve essere ortogonale nei confronti del vettore normale.
Pertanto, il prodotto scalare <v,n> è nullo.
$$ < P_1P , n > = 0 $$
Svolgo i calcoli del prodotto scalare
$$ < \begin{pmatrix} x -15\\ y \\ z \end{pmatrix} , \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} > = -5(x-15)-y+8z = 0 $$
$$ -5x+75-y+8z = 0 $$
Ho così trovato l'equazione cartesiana del piano
E così via
