Raggio vettore

Cos'è il raggio vettore

Posso rappresentare un punto P nello spazio tramite un vettore r $$ \vec{r} = x \cdot \hat{i} + y \cdot \hat{j} + z \cdot \hat{k} $$ dove x, y, z sono le coordinate cartesiane del punto (moti componenti) e i, j, k sono i versori degli assi cartesiani.

Il raggio vettore è anche detto vettore posizione.

Ai moti componenti posso anche aggiungere il tempo per studiare lo spostamento del punto nello spazio.

$$ \vec{r}(t) = x(t) \cdot \hat{i} + y(t) \cdot \hat{j} + z(t) \cdot \hat{k} $$

Il tempo è particolarmente utile per studiare i fenomeni fisici.

Nota. I versori sono i vettori unitari che determinano la direzione e il verso degli assi cartesiani di riferimento. Ad esempio, nello spazio a tre dimensioni i versori sono: $$ \hat{i} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \:\: \hat{j} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \:\: \hat{k} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} $$

La rappresentazione sul piano cartesiano

Dal punto di vista grafico il raggio vettore congiunge l'origine del piano cartesiano con le coordinate cartesiane del punto P(x,y,z).

Ad esempio, questo raggio vettore identifica il punto P sul piano.

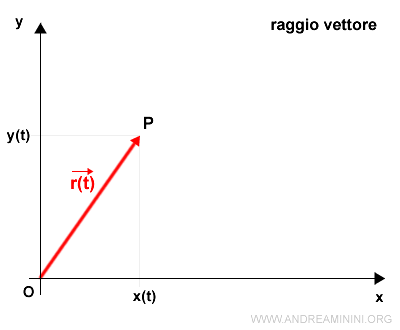
Nello spazio a tre dimensioni la rappresentazione è simile ma su tre assi cartesiani.

E così via.