Come rappresentare una retta con un vettore

Un vettore geometrico individua una direzione che accomuna tutte le rette del piano parallele al vettore.

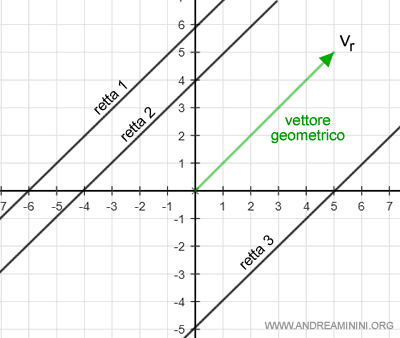
Pertanto, ogni retta del piano può essere descritta da:

• un vettore geometrico non banale v_r detto vettore direttore che indica la direzione della retta $$ v_r = \begin{pmatrix} l \\ m \end{pmatrix} $$

  I parametri l e m sono i parametri direttori della retta.

• un generico punto P₀ del piano in cui passa la retta. $$ P_0 = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} $$

  Esempio
  

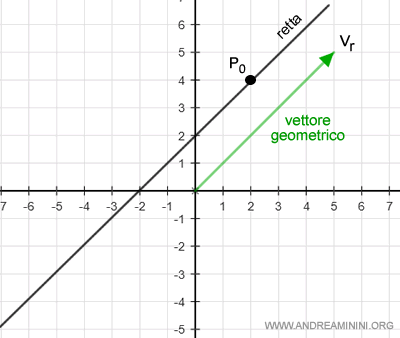
Un generico punto del piano appartiene alla retta se esiste un numero scalare alfa di R tale che

$$ OP = OP_0 + α v_r $$

Esempio

Il punto P₁ ha le coordinate (-5,-3).

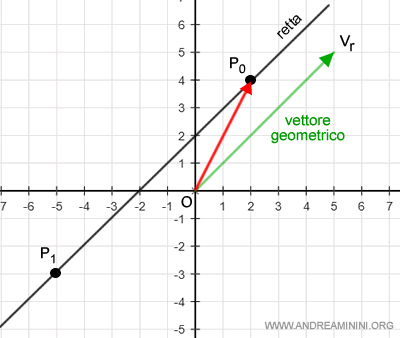
Il punto P₁ appartiene alla retta se

$$ OP_1 = OP_0 + α v_r $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + α \begin{pmatrix} 5 \\ 5 \end{pmatrix} $$

Risolvo il sistema di equazioni e verifico se esiste uno scalare alfa

$$ \begin{cases} -5 = 2 + α5 \\ -3 = 4 + α5 \end{cases} = \begin{cases} α = - \frac{7}{5} \\ α = - \frac{7}{5} \end{cases} $$

Il sistema si risolve con lo scalare alfa -7/5

Infatti

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + α \begin{pmatrix} 5 \\ 5 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 5α \\ 5α \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 5 \cdot ( - \frac{7}{5} ) \\ 5 \cdot ( - \frac{7}{5} ) \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} -7 \\ -7 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 - 7 \\ 4 - 7 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} -5 \\ -3 \end{pmatrix} $$

Posso generalizzare il risultato affermando che

Tutte le coordinate di tutti i punti della retta sono caratterizzati dalla seguente equazione, detta equazione vettoriale della retta: $$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + α \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$Trasformando l'equazione vettoriale in un sistema di equazioni, ottengo le equazioni parametriche della retta:$$ \begin{cases} x = x_0 + α l \\ y = y_0 +α m \end{cases} $$

Esistono infinite equazioni vettoriali ed equazioni parametriche perché esistono infiniti multipli del vettore direttore.

Le equazioni cartesiane

Il vettore P₀P₁ è parallelo al vettore direttore vr.

Secondo la teoria, un vettore è parallelo e proporzionale a un altro se

$$ \begin{pmatrix} x-x_0 & l \\ y - y_0 & m \end{pmatrix} \le 1 $$

Questo si verifica se

$$ det \begin{pmatrix} x-x_0 & l \\ y - y_0 & m \end{pmatrix} = 0 $$

che eseguendo i calcoli del determinante diventa

$$ m ( x-x_0 ) - l ( y - y_0 ) = 0 $$

Ho così ottenuto l'equazione cartesiana.

Anche in questo caso esistono infinite equazioni cartesiane.