Vettori ortogonali
I vettori ortogonali sono in relazione di ortogonalità (perpendicolarità) tra loro.
In uno spazio vettoriale reale due vettori v1,v2 sono ortogonali quando il loro prodotto scalare è nullo. $$ <v_1,v_2> = 0 $$
La relazione di ortogonalità tra due vettori è indicata con il simbolo di una T rovesciata.
$$ v_1 \perp v_2 $$
Nota. Il prodotto scalare pari a zero è una condizione necessaria ma non sufficiente di ortogonalità. E' necessario anche che i due vettori non siano vettori nulli ossia abbiano un modulo diverso da zero. Ad esempio, il prodotto scalare tra un vettore qualsiasi con un vettore nullo è pari a zero ma i due vettori non sono ortogonali. $$ < \vec{v} , \vec{0} > = 0 $$
Un esempio di vettori ortogonali
Nello spazio vettoriale V=R2 nel campo K=R ho due vettori:
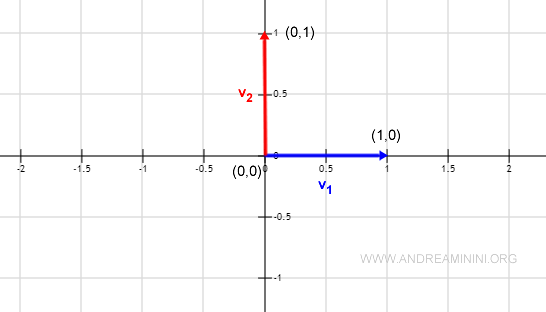
$$ v_1 = ( 1, 0 ) \\ v_2 = ( 0,1 ) $$
Il prodotto scalare <v1,v2> euclideo dei due vettori è uguale a zero.
$$ <v_1,v_2> = 1·0 + 0·1 = 0 $$
Quindi, i due vettori sono ortogonali.
Nota. Posso rappresentare i due vettori v1, v2 nel piano cartesiano prendendo come riferimento di partenza il punto O dell'origine (0,0). Osservando il grafico è subito evidente che i due vettori sono geometricamente perpendicolari tra loro.
Esempio 2
Ora prendo come esempio altri due vettori.
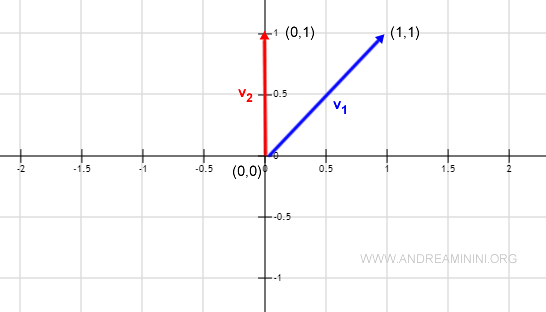
$$ v_1 = ( 1, 1 ) \\ v_2 = ( 0,1 ) $$
Il loro prodotto scalare è diverso da zero.
$$ <v_1,v_2> = 1·0 + 1·1 = 0+1 = 1 $$
Pertanto, i due vettori non sono ortogonali.
Nota. Anche in questo caso posso rappresentare i due vettori sul piano cartesiano ed è subito evidente che i due vettori non sono geometricamente perpendicolari tra loro.
Il coseno dell'angolo e l'ortogonalità
Quando i vettori sono entrambi diversi dal vettore nullo, c'è una stretta relazione tra i coseno dell'angolo formato dai vettori v1 e v2, il loro prodotto scalare e la norma.
$$ cos(v_1,v_2) = \frac{ <v_1,v_2> } { ||v_1|| \cdot ||v_2|| }$$
Per convenzione, se uno dei due vettori v1 e v2 è nullo si pone il coseno uguale a zero
$$ cos(v_1,v_2) := 0 \:\:se \:\:v_1=0_V \:\:o\:\: v_2=0_V $$
Un esempio pratico
Provo a calcolare il coseno dell'angolo di questi vettori:
$$ v_1 = ( 1, 0 ) \\ v_2 = ( 0,1 ) $$
Il loro prodotto scalare è
$$ <v_1,v_2> = 1·0 + 0·1 = 0 $$
Mentre le norme dei vettori sono:
$$ ||v_1|| = \sqrt{1^2+0^2} = 1 \\ ||v_2|| = \sqrt{0^2+1^2} = 1 $$
Quindi il coseno dell'angolo formato dai due vettori è
$$ cos(v_1,v_2) = \frac{ 0 } { 1 } = 0 $$
In effetti è un angolo di 90° e il coseno è uguale a 0.

Esempio 2
Ora provo a calcolare il coseno di altri due vettori:
$$ v_1 = ( 1, 1 ) \\ v_2 = ( 0,1 ) $$
Il loro prodotto scalare è
$$ <v_1,v_2> = 1·0 + 1·1 = 0+1 = 1 $$
Mentre le norme dei due vettori sono:
$$ ||v_1|| = \sqrt{1^2+1^2} = \sqrt{2} \\ ||v_2|| = \sqrt{0^2+1^2} = 1 $$
Quindi, il coseno dell'angolo formato tra i due vettori è
$$ cos(v_1,v_2) = \frac { 1 } { \sqrt{2} \cdot 1 } = \frac {1} { \sqrt{2} } $$
In effetti i due vettori formano un angolo di 45°

La differenza tra perpendicolarità e ortogonalità
Il termine ortogonalità è sinonimo di perpendicolarità.
Tuttavia, la parola "perpendicolarità" si utilizza più in ambito geometrico mentre "ortogonalità" è un concetto più astratto che si usa anche in ambiti non geometrici.
Le basi ortogonali e ortonormali
I vettori ortogonali compongono le basi ortogonali e ortonormali.
- La base ortogonale è composta da vettori ortogonali.
- La base ortonormale è una base ortogonale con vettori a norma unitaria.
