La regressione lineare

La regressione lineare è un metodo statistico utilizzato per modellare la relazione tra una variabile dipendente (risposta o output) e una o più variabili indipendenti (predittori o input).

Nella sua forma più semplice, la regressione lineare è una relazione lineare tra le variabili descritta dall'equazione:

$$ y = m x + q +  \epsilon $$

Dove:

• \( y \) è la variabile dipendente.
• \( x \) è la variabile indipendente.
• \( m \) è il coefficiente angolare (pendenza) che misura l’effetto di \( x \) su \( y \).
• \( q \) è l'intercetta, ovvero il valore di \( y \) quando \( x = 0 \).
• \( \epsilon \) è l'errore residuo o rumore, che rappresenta la differenza tra i valori osservati e quelli predetti.

Nella regressione lineare l'obiettivo è stimare i valori di \( m \) e \( q \) che minimizzano la somma dei quadrati delle differenze tra i valori osservati di \( y \) e quelli predetti dal modello (metodo dei minimi quadrati).

Una volta stimati questi parametri, posso usare l'equazione per fare previsioni o analizzare l’effetto delle variabili indipendenti sulla variabile dipendente.

L'origine del termine "regressione". Il termine "regressione" deriva dal lavoro di Francis Galton, un matematico e statistico del XIX secolo, che osservò come le altezze dei figli tendessero a "regredire" verso la media rispetto a quelle dei genitori. Notò che i figli di genitori molto alti tendevano a essere meno alti dei genitori, mentre i figli di genitori molto bassi tendevano a essere più alti dei genitori. In altre parole, l'altezza dei figli "regrediva" verso la media della popolazione. Originariamente la parola "regressione" indicava questa tendenza a ritornare verso un valore medio, ma oggi si usa per descrivere il metodo statistico che stima la relazione tra due o più variabili statistiche.

Come si calcola l'equazione della retta di regressione

Per calcolare una regressione lineare utilizzo il metodo dei minimi quadrati.

$$ y = m x + q +  \epsilon $$

L'obiettivo è trovare i coefficienti \( q \) (intercetta) e \( m \) (coefficiente angolare) che minimizzano la somma dei quadrati delle differenze tra i valori osservati (\( y_i \)) e quelli predetti \( \hat{y}_i \)).

Per prima cosa, calcolo le medie di \( x \) e \( y \):

$$ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \quad \text{e} \quad \bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i $$

Dove \( n \) è il numero di osservazioni.

Il coefficiente angolare \( m \) si calcola in questo modo:

$$ m = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2} $$

Questo coefficiente rappresenta l'inclinazione della retta e misura quanto cambia \( y \) per ogni unità di cambiamento in \( x \).

Poi calcolo l'intercetta \( q \) che indica il valore di \( y \) quando \( x = 0 \).

$$ q = \bar{y} - m \bar{x} $$

Quindi, l’equazione della retta di regressione è la seguente:

$$ \hat{y} = m x + q $$

Dove \( \hat{y} \) è il valore predetto dalla retta di regressione per ogni valore di \( x \).

Un esempio pratico

In questo esempio devo analizzare un piccolo insieme di dati.

Questa tabella mostra le variabili \( x \) (ore di studio) e \( y \) (punteggio ottenuto in un test):

Ore di studio (\( x \))	Punteggio (\( y \))
1	2
2	3
4	5
3	6
5	8

Calcolo le medie di \( x \) e \( y \)

$$ \bar{x} = \frac{1 + 2 + 4 + 3 + 5}{5} = 3 $$

$$ \bar{y} = \frac{2 + 3 + 5 + 6 + 8}{5} = 4.8 $$

Poi calcolo il coefficiente angolare \( m \) della retta di regressione usando questa formula:

$$ m = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2} $$

Svolgo i calcoli intermedi ottenendo \( (x_i - \bar{x}) \) e \( (y_i - \bar{y}) \):

\( x_i \)	\( y_i \)	\( x_i - \bar{x} \)	\( y_i - \bar{y} \)	\( (x_i - \bar{x})(y_i - \bar{y}) \)	\( (x_i - \bar{x})^2 \)
1	2	-2	-2.8	5.6	4
2	3	-1	-1.8	1.8	1
4	5	1	0.2	0.2	1
3	6	0	1.2	0	0
5	8	2	3.2	6.4	4

Infine calcolo la somma:

$$ \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) = 5.6 + 1.8 + 0.2 + 0 + 6.4 = 14 $$

$$ \sum_{i=1}^{n} (x_i - \bar{x})^2 = 4 + 1 + 1 + 0 + 4 = 10 $$

Sostituisco i risultati nella formula del coefficiente angolare.

$$ m = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2} $$

$$ m = \frac{14}{10} = 1.4 $$

Il coefficiente angolare $ m $ è anche detto coefficiente di regressione di Y rispetto a X, perché mi dice quanto varia la variabile Y al variare della variabile X.

Una volta ottenuto il coefficiente angolare $ m $, posso calcolare anche l'intercetta \( q \)

$$ q = \bar{y} - m \cdot \bar{x} $$

$$ q = 4.8 - 1.4 \times 3 = 4.8 - 4.2 = 0.6 $$

Infine, scrivo l’equazione della retta di regressione con i parametri $ m $ e $ q $ che ho appena calcolato.

$$ \hat{y} = 0.6 + 1.4x $$

Questa equazione mi permette di tracciare la retta di regressione e di predire il punteggio (\( y \)) basato sulle ore di studio (\( x \)).

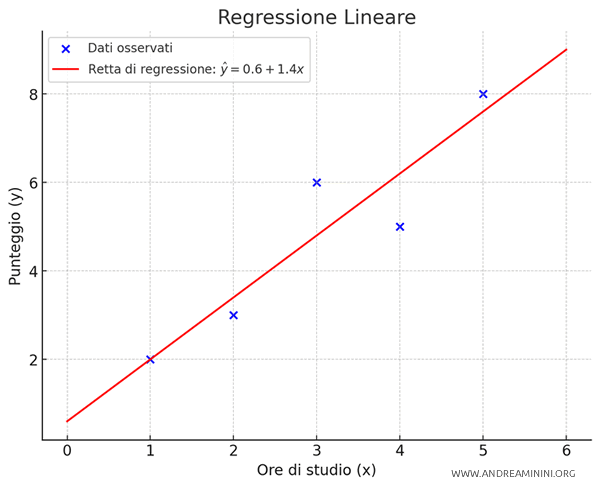
Ad esempio, se uno studente studia per 4 ore, il punteggio atteso è 6.2. $$ \hat{y} = 0.6 + 1.4 \times 4 = 0.6 + 5.6 = 6.2 $$

Esiste una relazione tra le ore di studio e il punteggio ottenuto in un test?

Finora ho calcolato la retta di regressione di Y rispetto a X.

Per verificare se c'è una relazione tra le variabili statistiche, devo calcolare anche la retta di regressione di X rispetto a Y utilizzando un procedimento simile.

$$ \hat{x} = m'y + q' $$

La media di ciascuna variabile è sempre la stessa:

$$ \bar{x} = \frac{1 + 2 + 4 + 3 + 5}{5} = 3 $$

$$ \bar{y} = \frac{2 + 3 + 5 + 6 + 8}{5} = 4.8 $$

Il coefficiente angolare \( m' \) per la regressione di \( X \) rispetto a \( Y \) si ottiene con la formula:

$$ m' = \frac{\sum_{i=1}^{n} (y_i - \bar{y})(x_i - \bar{x})}{\sum_{i=1}^{n} (y_i - \bar{y})^2} $$

Svolgo i calcoli intermedi in una tabella

\( x_i \)	\( y_i \)	\( x_i - \bar{x} \)	\( y_i - \bar{y} \)	\( (y_i - \bar{y})(x_i - \bar{x}) \)	\( (y_i - \bar{y})^2 \)
1	2	-2	-2.8	5.6	7.84
2	3	-1	-1.8	1.8	3.24
4	5	1	0.2	0.2	0.04
3	6	0	1.2	0	1.44
5	8	2	3.2	6.4	10.24

Poi sommo i dati ottenuti

$$ \sum_{i=1}^{n} (y_i - \bar{y})(x_i - \bar{x}) = 5.6 + 1.8 + 0.2 + 0 + 6.4 = 14 $$

$$ \sum_{i=1}^{n} (y_i - \bar{y})^2 = 7.84 + 3.24 + 0.04 + 1.44 + 10.24 = 22.8 $$

Quindi, sostituisco le sommatorie alla formula del coefficiente angolare:

$$ m' = \frac{\sum_{i=1}^{n} (y_i - \bar{y})(x_i - \bar{x})}{\sum_{i=1}^{n} (y_i - \bar{y})^2} $$

$$ m' = \frac{14}{22.8} \approx 0.614 $$

Il coefficiente angolare $ m' $ è detto coefficiente di regressione di X rispetto a X, perché mi dice quanto varia la variabile X al variare della variabile Y.

L'intercetta \( q' \) la calcolo utilizzando la formula:

$$ q' = \bar{x} - m' \bar{y} $$

$$ q' = 3 - 0.614 \times 4.8 \approx 3 - 2.9472 \approx 0.0526 $$

Con i valori ottenuti per \( m' \) e \( q' \), l'equazione della retta di regressione di \( X \) rispetto a \( Y \) è:

$$ \hat{x} = m'y + q' $$

$$ \hat{x} = 0.0526 + 0.614y $$

Questa equazione mi permette di stimare i valori di \( x \) in funzione di \( y \) utilizzando i dati osservati.

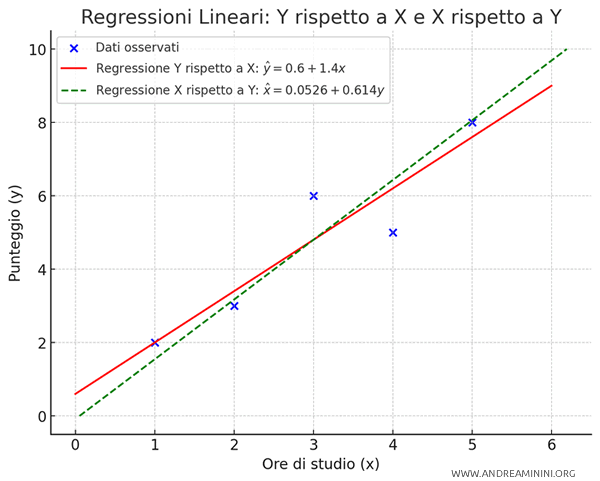
Il confronto tra la retta di regressione di Y rispetto a X (rossa) e la retta di regressione di X rispetto a Y (verde) mi permette di capire se c'è una relazione di dipendenza lineare tra le due variabili statistiche: le ore di studio e il punteggio ottenuto ai test.

• Se l'angolo tra le due rette è piccolo, esiste una relazione tra le due variabili. La regressione si dice "regressione perfetta" quando le due rette di regressione coincidono ovvero quando l'angolo tra le due rette è nullo.
• Se l'angolo tra le due rette tende a 90° (angolo retto), non c'è una dipendenza lineare tra le variabili

Quindi, se le due rette sono molto simili (in particolare, se i coefficienti angolari sono reciprocamente vicini), potrebbe indicare una relazione simmetrica o quasi lineare perfetta tra le due variabili.

In questo esempio l'angolo tra le due rette è molto piccolo, quindi esiste una dipendenza lineare tra le due variabili statistiche.

In altre parole, le ore di studio influiscono sul punteggio ottenuto sui test e dal punteggio ottenuto sul test posso dedurre le ore di studio.

E così via.