Il coefficiente di correlazione di Spearman
Il coefficiente di correlazione di rango di Spearman è una misura non parametrica della correlazione (o dipendenza monotona) tra due variabili. $$ r_s = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)} $$ dove \( d_i \) è la differenza tra i ranghi della coppia \( i \)-esima, \( n \) è il numero di osservazioni.
Si basa sui ranghi dei dati piuttosto che sui valori stessi delle variabili.
Il coefficiente di Spearman, indicato solitamente con \( \rho \) o \( r_s \), varia da -1 a 1:
- \( r_s = 1 \) indica una correlazione perfetta positiva, in cui i ranghi di entrambe le variabili si muovono insieme in modo monotono.
- \( r_s = -1 \) indica una correlazione perfetta negativa, con un andamento opposto dei ranghi.
- \( r_s = 0 \) indica assenza di correlazione, o nessuna relazione monotona.
Il calcolo di \( r_s \) si basa su una formula che considera la differenza tra i ranghi di ogni coppia di valori per le due variabili:
Cos'è il rango di un dato? Per "rango" si intende la posizione che un valore assume quando ordino i dati in ordine crescente (o decrescente) in una determinata variabile. Non importa la posizione originale nella sequenza non ordinata; conta solo l’ordine numerico. Ad esempio, considero la variabile $ X = \{ 8 , 6, 4, 2, 5, 7 \} $. I dati ordinati della variabile sono $ X_s = \{ 2, 4, 5, 6, 7, 8 \} $. Quindi, il valore 2 ha rango 1, il valore 4 ha rango 2, il valore 5 ha rango 3, e via dicendo.
Questo coefficiente è molto utile quando i dati non soddisfano le ipotesi della correlazione di Pearson, come la condizione di linearità e la normalità, poiché si concentra solo sull’ordine dei valori.
E' un buon indicatore per stimare la correlazione non lineare tra due variabili statistiche.
Un esempio pratico
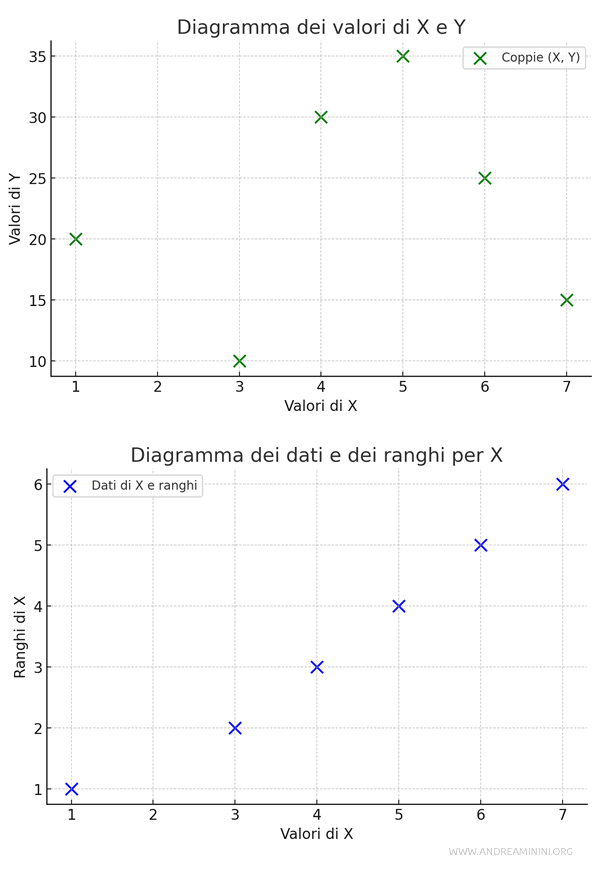
Ad esempio, ho i seguenti valori per le variabili \( X \) e \( Y \) per cinque individui:
| Individuo | \( X \) | \( Y \) |
|---|---|---|
| A | 15 | 10 |
| B | 20 | 25 |
| C | 25 | 30 |
| D | 35 | 20 |
| E | 30 | 35 |
Ordino i valori di \( X \) e assegno i ranghi, dove il valore più basso ottiene il rango 1 e così via.
- Per \( X \): \[15 \to 1, \, 20 \to 2, \, 25 \to 3, \, 30 \to 4, \, 35 \to 5\]
- Per \( Y \): \[10 \to 1, \, 20 \to 2, \, 25 \to 3, \, 30 \to 4, \, 35 \to 5\]
Ecco la tabella aggiornata con i ranghi:
| Individuo | \( X \) | Rango di \( X \) | \( Y \) | Rango di \( Y \) |
|---|---|---|---|---|
| A | 15 | 1 | 10 | 1 |
| B | 20 | 2 | 25 | 3 |
| C | 25 | 3 | 30 | 4 |
| D | 35 | 5 | 20 | 2 |
| E | 30 | 4 | 35 | 5 |
Ora calcolo la differenza \( d = \text{rango di } X - \text{rango di } Y \) per ogni individuo, quindi elevo ogni differenza al quadrato per ottenere \( d^2 \).
| Individuo | Rango di \( X \) | Rango di \( Y \) | \( d = X - Y \) | \( d^2 \) |
|---|---|---|---|---|
| A | 1 | 1 | 0 | 0 |
| B | 2 | 3 | -1 | 1 |
| C | 3 | 4 | -1 | 1 |
| D | 5 | 2 | 3 | 9 |
| E | 4 | 5 | -1 | 1 |
Infine, sommo i valori di \( d^2 \)
$$ \sum d^2 = 0 + 1 + 1 + 9 + 1 = 12 $$
A questo punto, uso la formula del coefficiente di Spearman per stimare la correlazione tra i dati.
$$ r_s = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)} $$
Dove \( \sum d_i^2 = 12 \) e \( n = 5 \)
$$ r_s = 1 - \frac{6 \cdot 12}{5 \cdot (5^2 - 1)} $$
$$ r_s = 1 - \frac{72}{120} $$
$$ r_s = 1 - 0.6 $$
$$ r_s = 0.4 $$
Il coefficiente di Spearman \( r_s = 0.4 \) indica una correlazione positiva moderata tra le variabili \( X \) e \( Y \).
Questo significa che, in generale, all'aumentare di \( X \) tende ad aumentare anche \( Y \), ma la relazione non è particolarmente forte.
Pro e contro del coefficiente di Spearman
Ecco i principali pro e contro del coefficiente di correlazione di Spearman:
A] Pro del coefficiente di Spearman
- Misura della relazione monotona
Spearman misura la dipendenza monotona tra due variabili, cioè se una variabile aumenta (o diminuisce) in modo coerente rispetto all'altra, indipendentemente dalla linearità della relazione. E' quindi un buon indicatore della correlazione non lineare tra i dati. - Robusto ai valori anomali
Essendo basato sui ranghi, il coefficiente di Spearman è meno influenzato dai valori estremi rispetto alla correlazione di Pearson. - Utilizzabile per dati ordinali
Spearman è adatto per dati ordinali o per situazioni in cui non si può assumere una distribuzione lineare o normale. - Semplice da interpretare
I valori di Spearman sono intuitivi, con 1 e -1 che indicano una correlazione perfettamente monotona positiva o negativa, e 0 che indica nessuna correlazione monotona.
B] Contro del coefficiente di Spearman
- Non rileva relazioni non monotone
Se le variabili sono correlate in modo complesso ma non monotono, Spearman non è in grado di rilevare la correlazione. Ad esempio, non individua relazioni quadratiche o sinusoidali. - Limitato ai ranghi
L'uso dei ranghi può ridurre la precisione, specialmente con piccoli dataset, dove l'assegnazione dei ranghi potrebbe non rappresentare bene la relazione tra i valori. - Non fornisce informazioni su ampiezza e direzione della variazione
Spearman mi dice solo se i dati salgono o scendono insieme, ma non mi dice niente sul ritmo di salita o discesa. Il coefficiente di Pearson, invece, mi dà un’idea più chiara della variazione effettiva in grandezza. - Perdita di informazioni sui dati originali
Lavorando solo sui ranghi, Spearman ignora la magnitudine dei dati, il che può essere uno svantaggio quando la relazione tra le variabili dipende dall’ampiezza dei valori stessi. - Il caso dei dati con lo stesso valore
Quando ho tanti dati con lo stesso valore (quindi stesso rango), Spearman fa fatica. Perché? Perché deve fare aggiustamenti, che smussano il risultato e possono renderlo meno preciso. - Sensibilità a cambiamenti nei ranghi
Spearman si basa solo sull'ordine, quindi piccole modifiche nell'ordinamento dei dati possono cambiarne il valore in modo drastico, specialmente coi dataset piccoli. Insomma, è un po' instabile se i dati non sono ben allineati.
E così via.
