I logaritmi

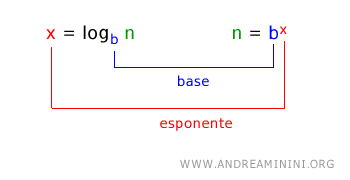
Il logaritmo di un numero reale n (detto argomento) è l'esponente x che posso dare a una base per ottenere il numero n. $$ x=\log_b n \Leftrightarrow b^x = n $$ Dove b > 0 , n > 0 sono numeri positivi e b ≠ 1

Il logaritmo si può vedere come un modo alternativo per scrivere una potenza.

poiché c'è una relazione stretta tra potenza e logaritmo

Ad esempio è equivalente scrivere

$$ 25=5^2 \Leftrightarrow 2 = \log_5 25 $$

Le condizioni di esistenza del logaritmo sono

• La base (b) deve essere un numero positivo diverso da uno.
• L'argomento (n) deve essere un numero positivo.

Per definizione la base e l'argomento sono numeri positivi.

Pertanto, non esiste il logaritmo di zero, né il logaritmo di un numero negativo.

Inoltre, la base deve essere diversa da 1 perché l'equazione 1^x=n è indeterminata.

Dimostrazione. Il logaritmo con base negativa non esiste perché l'esponenziale è definito solo per basi positive. $$ b>0 $$ Quindi, il logaritmo di un numero negativo non esiste perché se la base è maggiore di zero b>0 è impossibile trovare un numero x tale che b^x<0 $$ \forall \ x \in R \ , \ b>0 \Rightarrow b^x >0 $$ Il logaritmo con base zero non esiste perché il numero zero elevato per qualsiasi esponente x (escluso zero) è sempre uguale a zero. $$ 0^x = 0 \ \ \ con \ \ n \ne 0 $$ Il logaritmo di un numero n con base 1 non esiste in quanto per qualsiasi numero reale x la potenza di 1 è sempre uguale a 1. $$ 1^x = 1 $$

Il logaritmo x=log_b(n) è crescente al crescere dell'argomento n se la base b>1 è maggiore di uno

Viceversa, è decrescente se la base è compresa tra zero e uno 0<b<1.

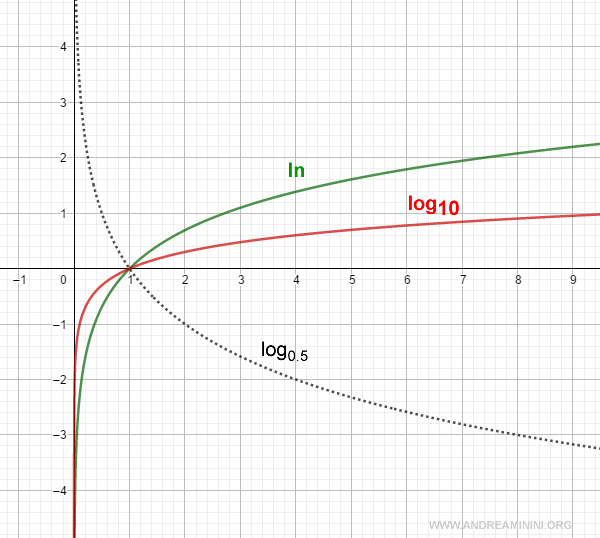
Nota. I logaritmi più usati in matematica, in ingegneria e nelle scienze sono il logaritmo su base 10 ( log₁₀ ) e il logaritmo naturale ( log_e ) su base 2.71828... ( numero di Nepero ).

Un esempio pratico

Questo logaritmo è su base 3

$$ x = \log_{3} 9 $$

Equivale a trovare il valore dell'incognita x in questa equazione esponenziale

$$ 3^x = 9 $$

Pertanto, il logaritmo è x=2

$$ x = \log_{3} 9 = 2 $$

perché

$$ 3^2 = 9 $$

Osservazioni

Alcune ossservazioni utili sui logaritmi

• Il logaritmo è uguale a 1 quando la base e l'argomento coincidono perché b¹=b $$ \log_b b = 1 $$

  Esempio. $$ log_5 5 = 1 $$ perché $$ 5^1 = 5 $$

• Il logaritmo di uno è uguale a zero quando b⁰=1 $$ \log_b 1 = 0 $$

  Esempio. $$ log_5 1 = 0 $$ perché $$ 5^0 = 1 $$

• La base (b) elevata al logaritmo di base b del numero n è il numero n stesso $$ b^{\log_b n} = n $$ Poiché se b^x=n allora x = log_b n
  

  Esempio. $$ 5^{\log_5 25} = 25 $$

• Dati due numeri positivi uguali x=y allora anche i rispettivi logaritmi rispetto alla stessa base sono uguali e viceversa $$ x=y \Leftrightarrow \log_b x = \log_b y $$

La storia dei logaritmi

L'utilizzo delle potenze risale alle prime civiltà umane nel II millennio a.C.

I primi tentativi senza successo di trovare a quale esponente debba essere elevato un numero per ottenere una potenza risalgono alle civiltà mesopotamiche.

Il problema venne risolto molto tempo dopo, nel XVI secolo, dal matematico scozzese Nepero ( John Napier ) e dallo svizzero J. Burgi.

Nepero fu il primo a usare il termine "logaritmo" e a stilare le prime tavole logaritmiche.

Pochi anni dopo il matematico inglese Henry Briggs introdusse i logaritmi su base 10 ( logaritmi decimali ), perché considerati più semplici e utili.

Nel corso del tempo le tavole periodiche vennero ampliate su più potenze e più basi.

Nel XVIII secolo il matematico Eulero ( Leonhard Euler ) fu il primo a utilizzare il numero di Nepero e=2,71828 come base dei logaritmi per definire le potenze con esponente immaginario.

Pertanto, a Eulero si deve la nascita dei logaritmi naturali.

A Eulero si deve anche l'idea che il logaritmo è l'operazione inversa dell'esponenziale e viceversa.

E così via.