Glissometria

La glissometria è una trasformazione geometrica del piano che si ottiene come composizione di una simmetria assiale rispetto a una retta $r$ con una traslazione $T_{\vec{v}}$ che ha come direzione un vettore parallelo $\vec{v}$ all’asse di simmetria. $$ G = T_{\vec{v}} \circ S_r $$

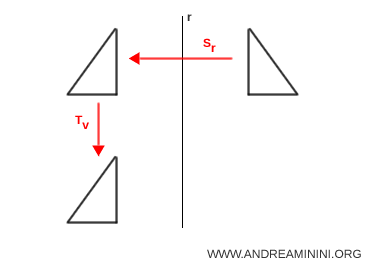
La glissometria è una trasformazione isometrica, cioè conserva le distanze tra i punti.

Tuttavia, non coincide con nessuna delle trasformazioni elementari considerate singolarmente.

Non è una simmetria assiale pura, perché non esiste una retta che rimanga fissa: ogni punto del piano viene spostato in una posizione diversa.

Non è neppure una traslazione semplice, poiché la presenza della riflessione comporta sempre un’inversione dell’orientamento della figura.

Nota. Ci sono alcuni casi particolari banali che fanno eccezione alla regola.  Se il vettore di traslazione è nullo ($\vec{v}=0$), la glissometria coincide con la sola simmetria assiale. Se invece la simmetria è assente, resta soltanto la traslazione.

Un esempio pratico

Considero il piano cartesiano, una simmetria assiale e una traslazione

• La simmetria assiale ha come asse di simmetria la retta $r: x=0$ ossia l’asse $y$.
• La traslazione si basa sul vettore $\vec{v} = (0,2)$, quindi parallelo a $r$.

Prendo il punto $P(3,1)$.

Con la simmetria assiale rispetto a $r$, il punto diventa $P'(-3,1)$.

Poi, applico la traslazione di $\vec{v}$, ottenendo $P''=(-3,1+2) = (-3,3)$.

Il punto $P$ è stato trasformato in $P''$ dalla glissometria.

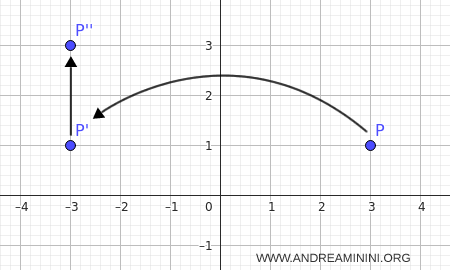
Geometricamente, una glissometria appare come un “scivolamento riflesso”: si riflette la figura rispetto a un asse, poi la si fa scorrere parallelamente all’asse stesso.

Note

Alcune note aggiuntive sulla glissometria

• Assenza di punti uniti
  In una glissometria non esistono punti che rimangano fissi (punti uniti), a differenza della simmetria assiale in cui i punti appartenenti all’asse restano invariati. In questo caso ogni punto del piano viene spostato. L’unica entità che si conserva globalmente è la retta dell’asse di simmetria che, pur non lasciando fissi i singoli punti, viene trasformata su sé stessa dalla glissometria.

E così via.