Teorema: il diametro è maggiore di ogni corda che non attraversa il centro.

In una circonferenza ogni diametro ha una lunghezza maggiore di qualsiasi corda che non passa per il centro.

La dimostrazione

Considero una circonferenza con centro O, una corda AB non passante per il centro e un diametro CD.

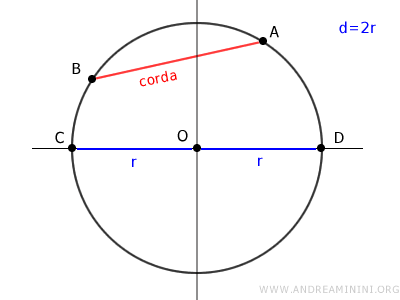
I punti O, A, B formano un triangolo rettangolo OAB.

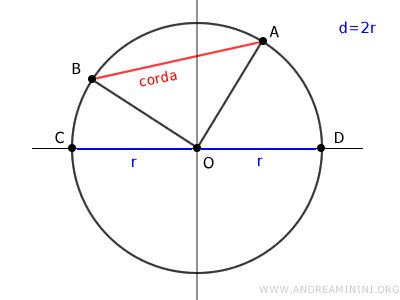
Secondo il teorema della disuguaglianza triangolare, in un triangolo ogni lato è minore della somma degli altri due lati.

Quindi, la corda AB è minore della somma di OA e OB.

$$ \overline{AB} < \overline{OA} + \overline{OB} $$

I due lati OA e OB hanno ciascuno la stessa lunghezza del raggio della circonferenza ossia OA=r e OB=r.

Quindi, posso riscrivere la disequazione in questa forma equivalente sostituendo i lati OA e OB con il raggio (r) della circonferenza.

$$ \overline{AB} < r + r $$

$$ \overline{AB} < 2r $$

Sapendo che il segmento CD è il diametro (d) della circonferenza ed è congruente con la somma di due raggi, ossia CD=2r, posso sostituire 2r con il diametro (d) della circonferenza

$$ \overline{AB} < 2r $$

Inoltre, sapendo che il diametro d=2r è il doppio del raggio

$$ \overline{AB} < d $$

Questo dimostra che una corda non passante per il centro della circonferenza è minore del diametro (d).

Dimostrazione alternativa

Considero una circonferenza con centro O, una corda AB che non passa per il centro e un diametro CD.

Traccio il segmento OB

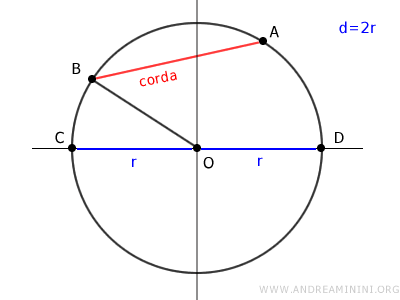
Traccio un raggio della circonferenza che passa per il punto medio E della corda AB

Sapendo che l'asse di una corda passa sempre per il centro di una circonferenza, deduco che un raggio che biseca una corda è perpendicolare alla corda stessa.

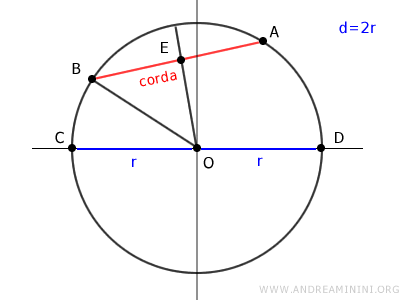
Pertanto, il triangolo OBE è un triangolo rettangolo

Secondo il teorema di Pitagora, in un triangolo rettangolo l'ipotenusa è sempre maggiore rispetto a ogni cateto. Quindi OB>BE

$$ \overline{OB} > \overline{BE} $$

Per la proprietà invariantiva moltiplico per due entrambi i membri della disequazione

$$ 2 \cdot \overline{OB} > 2 \cdot \overline{BE} $$

Sapendo che OB=r è uguale al raggio, il doppio del raggio 2r=CD è uguale al diametro (d).

$$ \overline{CD} > 2 \cdot \overline{BE} $$

Sapendo che E è il punto medio della corda AB, allora 2BE è congruente con la corda AB.

$$ \overline{CD} > \overline{AB} $$

Questo dimostra che il diametro (CD) è sempre maggiore di una corda (AB) che non passa per il centro della circonferenza.

E così via.