Il teorema del diametro perpendicolare a una corda
Se in una circonferenza un diametro è perpendicolare a una corda, allora la corda, l'angolo al centro e l'arco corrispondente sono divisi a metà.
La dimostrazione
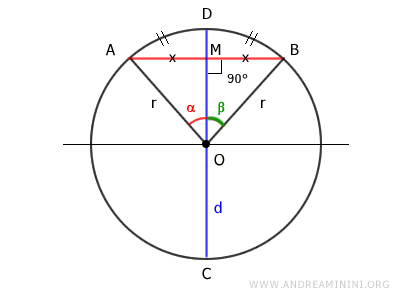
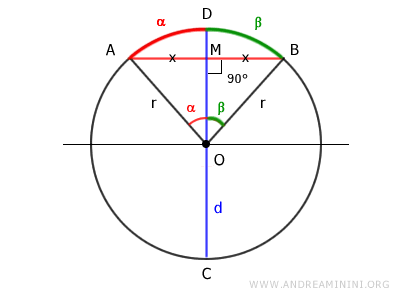
Considero una circonferenza con centro O, una corda AB e un diametro CD.
Per ipotesi iniziale il diametro è perpendicolare alla corda.
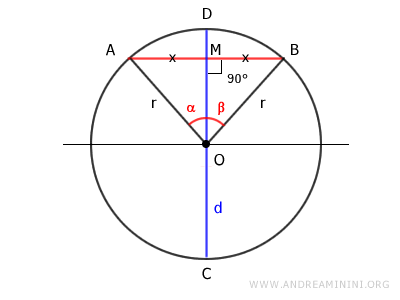
Traccio i lati OA e OB.
In questo modo ottengo un triangolo OAB.
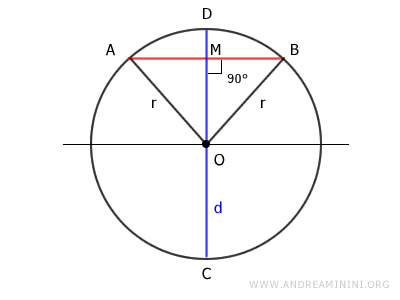
Il segmento OM è l'altezza del triangolo, in quanto è parte del diametro CD e per l'ipotesi iniziale il diametro è perpendicolare alla corda.
I segmenti OA e OB sono ciascuno uguali al raggio, ossia OA=r e OB=r, quindi sono congruenti tra loro OA≅OB
Essendo OA≅OB due lati congruenti, il triangolo OAB è un triangolo isoscele.

In un triangolo isoscele la mediana coincide con l'altezza OM.
Quindi, l'estremo M è il punto medio del segmento AB che lo divide in due segmenti congruenti AM=MB.
Questo dimostra che la corda AB viene divisa a metà dal diametro.
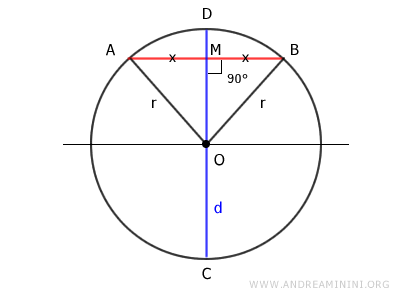
Inoltre, in un triangolo isoscele anche la bisettrice coincide con l'altezza OM.
Pertanto, l'angolo al centro viene diviso a metà in due angoli congruenti α≡β.

Sapendo che in una circonferenza a due angoli al centro congruenti α≅β corrispondono due archi congruenti AD≅BD, anche l'arco viene diviso a metà.
E così via.
