Teorema delle corde equidistanti dal centro
In una circonferenza due corde congruenti hanno la stessa distanza dal centro, e viceversa.
Vale anche il teorema inverso, ossia due corde equidistanti dal centro sono congruenti.
La dimostrazione
La dimostrazione è suddivisa in due parti
A] Due corde equidistanti dal centro sono congruenti
Devo dimostrare che due corde equidistanti dal centro O della circonferenza sono congruenti tra loro.
Considero una circonferenza e due corde AB e CD equidistanti dal centro O della circonferenza.
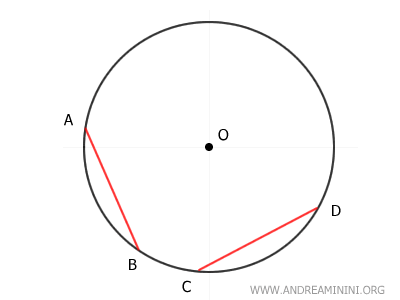
Traccio la distanza dei segmenti rispetto al centro della circonferenza (O).
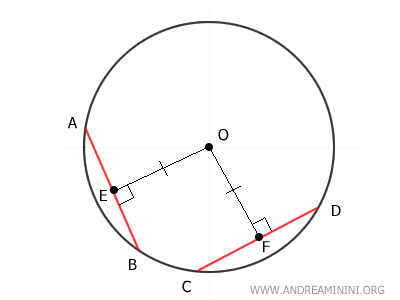
Nota. La distanza è un segmento perpendicolare al segmento AB (o CD) che ha per estremo il centro O della circonferenza.
Per ipotesi iniziale, i due segmenti hanno la stessa distanza dal centro O
$$ \overline{OE} \cong \overline{OF} $$
Traccio i segmenti OB e OD che essendo due raggi della circonferenza, sono segmenti congruenti tra loro.
$$ \overline{OB} \cong \overline{OD} $$
In questo modo ottengo due triangoli rettangolo OBE e ODF.
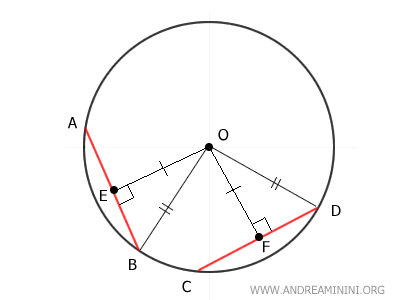
I due triangoli rettangolo sono congruenti perché hanno due cateti congruenti OB≅OD e OE≅OF.
$$ OBE \cong ODF $$
Essendo due triangoli congruenti, hanno i lati e gli angoli congruenti nello stesso ordine.
In particolar modo mi interessa sapere che sono congruenti i cateti BE≅DF
$$ \overline{BE} \cong \overline{DF} $$
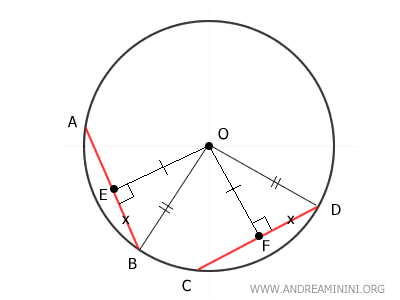
A questo punto traccio anche due segmenti OA e OC, ottenendo due triangoli OAB e OCD.
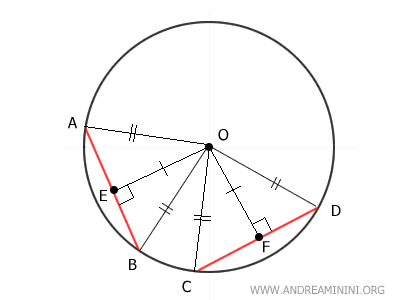
Essendo OA e OC due raggi della circonferenza, sono congruenti tra loro OA≅OC e sono congruenti con gli altri raggi OB e OD
$$ \overline{OA} \cong \overline{OC} \cong \overline{OC} \cong \overline{OD} $$
Pertanto, i triangoli AOB e COD sono due triangoli isosceli perché hanno due lati congruenti OA≅OB e OC≅OD.
Sapendo che in un triangolo isoscele l'altezza coincide con la mediana, deduco che che i segmenti AE≅BE e CF≅DF sono congruenti.
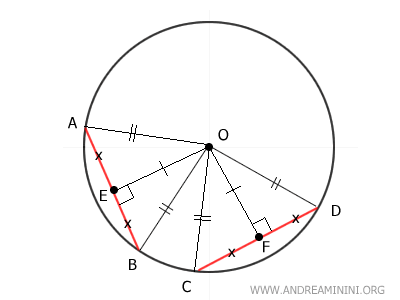
Sapendo già che BE≅DF deduco che anche il doppio dei segmenti 2BE≅2DF è congruente.
Poiché 2BE è la corda AB (ossia 2BE≅AB) e 2DF è la corda CD (ossia 2DF≅CD), deduco che le due corde AB≅CD sono congruenti.
$$ \overline{AB} \cong \overline{CD} $$
Questo dimostra che due corde equidistanti dal centro O della circonferenza sono due corde congruenti tra loro.
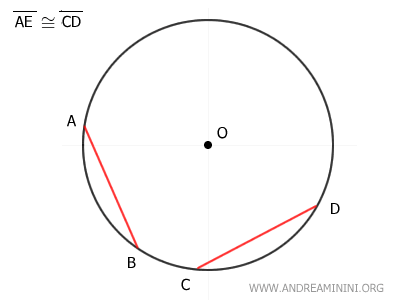
B] Due corde congruenti sono equidistanti dal centro della circonferenza
Considero due corde AB e CD congruenti per ipotesi AB≅CD.
Traccio i segmenti OA, OB, OC e OD che essendo raggi sono tutti congruenti tra loro OA≅OB≅OC≅OD.

I due triangoli OAB e OCD sono congruenti per il terzo criterio di congruenza (LLL).
$$ OAC = OCD $$
Inoltre, i triangoli OAB E OCD sono due triangoli isosceli, perché hanno due lati congruenti OA≅OB e OC≅OD.
Nei triangoli isosceli la mediana coincide con l'altezza, ovvero con il segmento che unisce un vertice con il punto medio del lato opposto.
In questo caso, i segmenti OE e OF sono le altezze dei triangoli e sono congruenti tra loro OE≅OF perché i due triangoli sono congruenti.
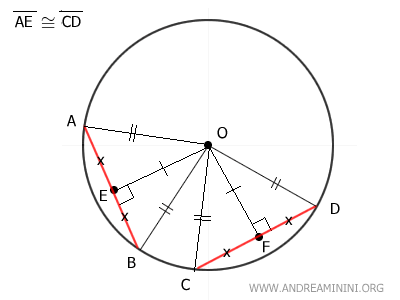
Le altezze OE≅OF dei due triangoli sono segmenti perpendicolari alle corde che partono dal centro O della circonferenza. Pertanto, questi segmenti rappresentano la distanza delle corde dal centro.
Questo dimostra che le due corde congruenti sono equidistanti dal centro della circonferenza.
E così via.
