Teorema delle corde non congruenti

In una circonferenza due corde non congruenti, non sono equidistanti dal centro. La corda più corta ha una distanza maggiore e viceversa.

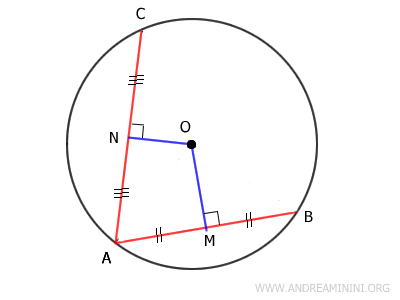
La dimostrazione

Traccio due corde non congruenti AB e AC nella circonferenza dove AC è più lunga di AB ossia AB>AC

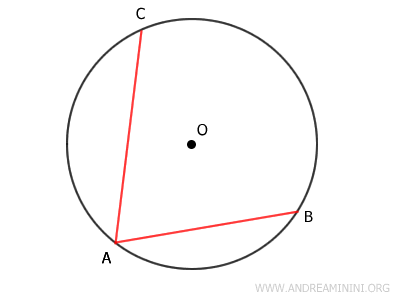
Traccio i raggi OA, OB e OC che, ovviamente, sono congruenti tra loro OA≅OB≅OC, perché la circonferenza è il luogo geometrico dei punti equidistanti dal centro O.

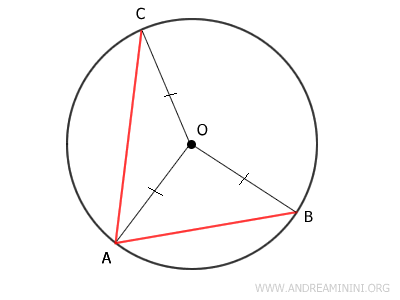
In questo modo ottengo due triangoli AOB e AOC.

I due triangoli AOB e AOC sono entrambi dei triangoli isosceli perché hanno due lati obliqui congruenti.

Essendo due triangoli isosceli, la mediana coincide con l'altezza. Quindi, i punti M e N sono i punti medi rispettivamente della corda AB e AC.

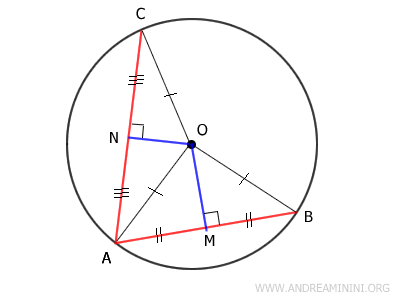
Traccio un segmento MN che congiunge i punti medi M e N.

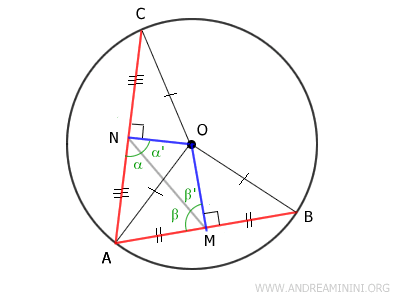
Il segmento MN forma due coppie di angoli complementari.

$$ \alpha + \alpha ' = 90° $$

$$ \beta + \beta ' = 90° $$

Nel triangolo AMN il lato AN è maggiore del lato AM perché, per l'ipotesi iniziale, la corda AC>AB. Sapendo che il segmento AN è la metà di AC e AN è la metà di AB, deduco che AN>AM

$$ \overline{AN} > \overline{AM} $$

Nel triangolo AMN se il lato AN è maggiore di AM, allora anche i rispettivi angoli opposti hanno la stessa relazione d'ordine.

Al lato AN si oppone l'angolo β mentre al lato AM si oppone l'angolo α.

$$ \beta > \alpha $$

Quindi, sapendo che α+α'=90° e β+β'=90° negli angoli complementari α' e β' la relazione d'ordine si inverte

$$ \beta ' < \alpha ' $$

Infine, sapendo che β'<α' nel triangolo OMN, deduco per lo stesso teorema precedente che anche i rispettivi lati opposti hanno la stessa relazione d'ordine ON<OM

Pertanto, deduco che il segmento OM è maggiore del segmento ON

$$ \overline{OM} > \overline{ON} $$

Questo dimostra che la corda più corta AB ha una distanza maggiore OM>ON dal centro della circonferenza O rispetto alla corda più lunga AC.

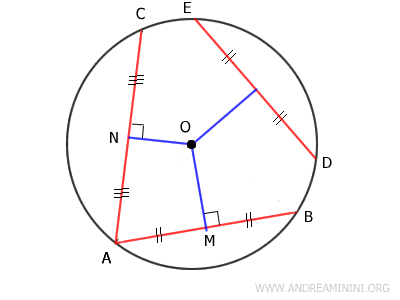
Sapendo che ogni corda DE≅AB congruente con AB ha la stessa distanza dal centro, deduco che qualsiasi corda più corta di AC ha una distanza maggiore dal centro.

E così via.