Il teorema del diametro passante nel punto medio di una corda

Se in una circonferenza il diametro interseca il punto medio di una corda che non passa per il centro, allora il diametro è perpendicolare alla corda.

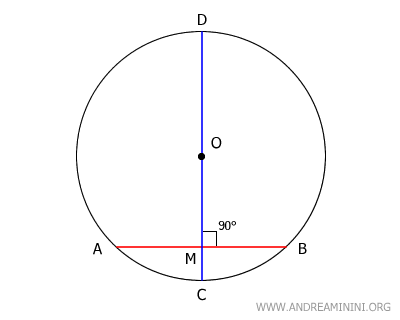
La dimostrazione

Considero una corda AB che non attraversa per il centro della circonferenza O e un diametro CD che interseca il punto medio M della corda.

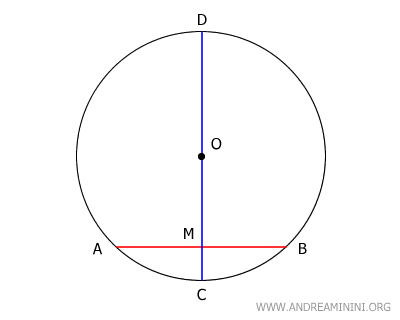
Traccio due segmenti AO e BO che congiungono gli estremi della corda A e B con il centro O, formando un triangolo ABO.

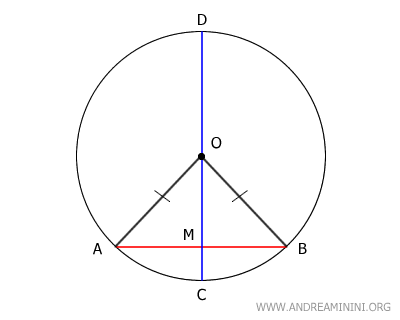
Poiché i segmenti AO e BO sono entrambi raggi della circonferenza, sono congruenti:

$$ \overline{AO} \cong \overline{BO} $$

Pertanto, avendo due lati congruenti, il triangolo ABO è un triangolo isoscele.

In un triangolo isoscele, la mediana tracciata dal vertice verso il lato opposto coincide con l'altezza, la bisettrice e l'asse.

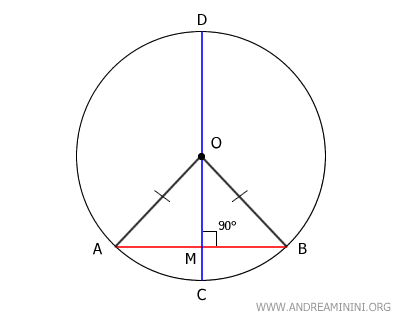
In questo caso il segmento OM è la mediana e, quindi, è anche l'altezza del triangolo. Di conseguenza, OM forma un angolo retto (90°) con AB.

Poiché il segmento OM è parte del diametro CD, posso concludere che il diametro CD è perpendicolare alla corda AB.

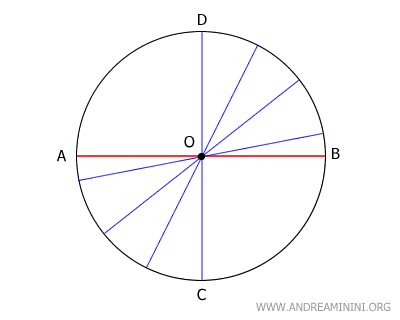
Nota. È fondamentale sottolineare che questo teorema è valido solo quando la corda AB non attraversa il centro O della circonferenza. Se la corda dovesse intersecare O, il suo punto medio coinciderebbe "sempre" con il centro della circonferenza. In tal caso, ogni diametro attraverserebbe il centro formando angoli di varia ampiezza. In pratica, il punto O diventerebbe il centro di un fascio di rette.

E così via