Le trasformazioni di Lorentz

Le trasformazioni di Lorentz descrivono come cambiano le coordinate spazio-temporali di un evento quando si passa da un sistema di riferimento inerziale a un altro in moto rettilineo uniforme rispetto al primo.

Queste trasformazioni sono fondamentali nella teoria della relatività ristretta di Einstein, perché garantiscono che le leggi della fisica e in particolare la velocità della luce nel vuoto, rimangano invarianti in tutti i sistemi inerziali.

Si applicano solo in caso di sistemi inerziali e relatività.

Cos'è un sistema inerziale?

Un sistema inerziale è un sistema di riferimento nel quale vale la legge d’inerzia, ossia la prima legge di Newton: un corpo libero, non soggetto a forze, mantiene il suo stato di moto rettilineo uniforme.

Cosa afferma la relatività ristretta?

La relatività ristretta afferma che

• nessun sistema inerziale è privilegiato rispetto agli altri sistemi inerziali
• le leggi fisiche devono avere la stessa forma in tutti i sistemi inerziali, sia quelli che si muovono a velocità costante, sia quelli in stato di quiete.
• la velocità della luce nel vuoto è costante e uguale per ogni osservatore

Da questo deduco che la luce non ha bisogno di un “mezzo” immobile (etere) per propagarsi e che non esiste un punto fisso dell’universo rispetto al quale misurare i movimenti assoluti.

Le formule delle trasformazioni di Lorentz

Considero due osservatori (o sistemi):

• $S$: sistema di riferimento "fermo"
• $S'$: sistema che si muove a velocità costante $v$ lungo l’asse $x$

Per semplicità, assumo che il moto avvenga lungo l’asse x, così le altre componenti spaziali y e z restano costanti.

Un evento che si verifica nel sistema $ S $ alle coordinate $(x, y, z, t)$, ha come coordinate $(x', y', z', t')$ nel sistema $S'$ secondo le trasformazioni di Lorentz:

$$
\begin{cases}
x' &= \gamma (x - vt) \\
y' &= y \\
z' &= z \\
t' &= \gamma \left(t - \frac{v}{c^2} x\right)
\end{cases}
$$

Dove il fattore di Lorentz $ \gamma $ è determinato dalla seguente formula:

$$ \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} $$

Come si può notare, quando la velocità è molto bassa ( $v \ll c$ ) il fattore $\gamma \approx 1$ tende a 1, e si torna alle trasformazioni classiche di Galileo.

Che cosa diceva Galileo? Galileo formulò le trasformazioni classiche del moto che oggi chiamiamo "trasformazioni galileiane". Queste valgono solo nel caso in cui le velocità coinvolte siano molto piccole rispetto alla velocità della luce ($v \ll c$). Nelle trasformazioni di Galileo se un sistema $S'$ si muove con velocità costante $v$ lungo l’asse $x$ rispetto a un sistema $S$, allora le coordinate di un evento si trasformano così: $$ \begin{cases} x' &= x - vt \\ y' &= y \\ z' &= z \\ t' &= t \end{cases} $$ In questo caso lo spazio cambia in base al moto relativo: la posizione $x'$ dipende da quanto si è spostato il sistema, il tempo è uguale per tutti: $t' = t$ ed è assoluto, ossia è indipendente dal sistema di riferimento. In breve, Galileo affermava che il tempo scorre uguale per tutti e che le velocità si sommano. Questo funziona bene per oggetti lenti. Ma quando le velocità si avvicinano a quella della luce, queste regole non valgono più e serve la relatività ristretta.

Effetti relativistici

Le trasformazioni di Lorentz hanno conseguenze osservabili e sperimentalmente verificate. Di seguito, i principali effetti.

• Relatività della simultaneità

  Due eventi che si verificano nello stesso istante (eventi simultanei) ma in punti diversi nel sistema inerziale $S$ non sono simultanei anche nel sistema $S'$.

  Gli eventi sono simultanei in entrambi i sistemi inerziali S e S' solo nel caso in cui avvengono nello stesso punto spaziale. Pertanto, si può concludere che la simultaneità degli eventi non è una proprietà assoluta, ma dipende dal sistema di riferimento. 

  Esempio. Due lampi colpiscono contemporaneamente le due estremità di un treno in movimento per un osservatore a terra (sistema di riferimento S). Un passeggero seduto al centro del convoglio, invece, non li percepisce come simultanei.
  
  Infatti, nel sistema del treno (S') i raggi luminosi devono raggiungere un osservatore che si sta muovendo: il fronte d’onda proveniente dall’estremità anteriore gli va incontro, mentre quello proveniente dall’estremità posteriore deve inseguirlo. Di conseguenza, i due segnali non lo raggiungono nello stesso istante. È opportuno sottolineare che questa discrepanza non è un semplice effetto ottico, ma la manifestazione concreta del fatto che la simultaneità definita in $S$ (osservatore a terra) non coincide con quella definita in $S'$ (passeggero sul treno).

  Dimostrazione

  Considero due sistemi inerziali $S$ e $S'$, con $S'$ in moto uniforme a velocità $v$ lungo l’asse $x$ rispetto a $S$. Le trasformazioni di Lorentz stabiliscono la relazione tra le coordinate di un evento nei due sistemi: $$ t' = \gamma \left( t - \frac{v}{c^2}x \right), $$ dove $$ \gamma = \frac{1}{\sqrt{1 - v^2/c^2}}$$ Per ipotesi, suppongo ora che in $S$ avvengano due eventi $A$ e $B$, situati in punti distinti $x_A \neq x_B$, ma nello stesso istante: $$ t_A = t_B. $$ Essendo eventi simultanei la differenza della variabile tempo è nulla $ t_A - t_B = 0 $ Applicando la trasformazione temporale, ottengo i tempi corrispondenti in $S'$: $$ t'_A = \gamma \left( t_A - \frac{v}{c^2}x_A \right), \quad t'_B = \gamma \left( t_B - \frac{v}{c^2}x_B \right) $$ Poi verifico se sono simultanei $$ t'_A - t'_B = \gamma \left( t_A - \frac{v}{c^2}x_A \right) - \gamma \left( t_B - \frac{v}{c^2}x_B \right) $$ $$ t'_A - t'_B = \gamma t_A - \gamma \frac{v}{c^2}x_A  - \gamma  t_B + \gamma \frac{v}{c^2}x_B $$  Poiché $t_A = t_B$ per ipotesi iniziale, risulta $ \gamma t_A = \gamma t_B$ $$ \require{cancel}  t'_A  - t'_B = \cancel{ \gamma t_A } - \gamma \frac{v}{c^2}x_A  - \cancel{ \gamma  t_B } + \gamma \frac{v}{c^2}x_B $$ $$ t'_A - t'_B = - \gamma \frac{v}{c^2}x_A  + \gamma \frac{v}{c^2}x_B $$ $$ t'_A - t'_B = \gamma \frac{v}{c^2}(x_B - x_A) $$ Quindi, la differenza temporale $ t'_A - t'_B $ in $S'$ è proporzionale alla differenza spaziale $ x_B - x_A $ in $S$. Da ciò consegue che, se gli eventi sono simultanei in $S$ ma si trovano in luoghi diversi, in $S'$ non risultano simultanei. La simultaneità è preservata nei due sistemi soltanto quando gli eventi avvengono nello stesso punto spaziale ($x_A = x_B$). In tutti gli altri casi, il tempo di accadimento dipende dal sistema di riferimento.
• Contrazione delle lunghezze
  Un oggetto ha lunghezza propria $L'$ nel sistema $S'$ in cui è a riposo, ossia dove si trova. Se $S'$ si muove rispetto a un altro sistema inerziale $S$, allora, dal punto di vista di un osservatore in $S$, la lunghezza dell’oggetto risulta contratta lungo la direzione del moto. $$ L = \frac{L'}{\gamma} $$ La contrazione avviene solo nella direzione del moto. Le dimensioni trasversali restano invariate.

  Esempio. Un'asta lunga 2 metri a riposo in $S'$, vista da un osservatore in $S$ che  vede $S'$ muoversi a $0.8c$, appare lunga 1.2 metri. $$ \gamma = \frac{1}{\sqrt{1 - 0.8^2}} = \frac{1}{0.6} = 1.666... $$ $$
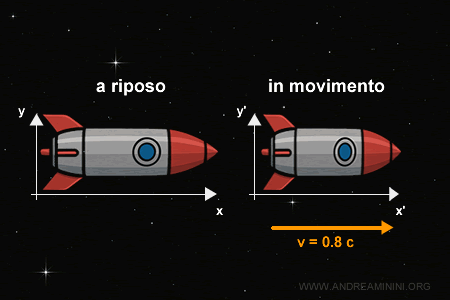
  L = \frac{2}{1.666...} \approx 1.2 \text{ metri} $$ Lo stesso accade in un missile che viaggia nello spazio a velocità prossime a quella della luce, la lunghezza lungo la direzione di moto si accorcia dal punto di vista di un osservatore esterno, mentre le altre dimensioni trasversali restano immutate.
  

  Dimostrazione della contrazione delle lunghezze

  Considero un’asta rigida di lunghezza propria $L'$, posta lungo l’asse $x'$ nel sistema $S'$ in cui è a riposo.

  Le coordinate delle due estremità sono quindi

  $$ x'_A = 0, \qquad x'_B = L' $$

  In questo sistema la distanza tra i due estremi, rilevata in qualunque istante $t'$, è semplicemente

  $$ L' = x'_B - x'_A $$

  Suppongo ora di misurare la lunghezza della stessa asta da un sistema inerziale $S$, nel quale l’asta si muove con velocità $v$ lungo l’asse $x$.

  Per determinare la lunghezza in $S$ devo registrare le posizioni delle estremità nello stesso istante temporale $t$ secondo gli orologi di $S$.

  Le trasformazioni di Lorentz collegano le coordinate spaziali dei due sistemi:

  $$ x' = \gamma (x - vt), \qquad t' = \gamma \left(t - \frac{v}{c^2}x\right) $$

  Dove il fattore di Lorentz è

  $$ \gamma = \frac{1}{\sqrt{1 - v^2/c^2}} $$

  Per l’estremo $A$, posto a $x'_A = 0$, risulta

  $$ x'_A = 0 = \gamma (x_A - vt) $$

  $$ \frac{ 0 }{ \gamma } =  x_A - vt $$

  $$ x_A - vt = 0 $$

  $$ x_A = vt $$

  Per l’estremo $B$, posto a $x'_B = L'$, si ha

  $$ x'_B = L' = \gamma (x_B - vt)  $$

  $$  \frac{L'}{\gamma} = x_B - vt  $$

  $$  x_B = vt + \frac{L'}{\gamma}   $$

  Poiché la misura in $S$ richiede lo stesso istante $t$ per entrambi gli estremi, la distanza misurata è

  $$ L = x_B - x_A = \left(vt + \frac{L'}{\gamma}\right) - (vt) = \frac{L'}{\gamma} $$

  La lunghezza rilevata in $S$ è minore della lunghezza propria $L'$ di un fattore $\gamma$. 

  $$ L = x_B - x_A =  \frac{L'}{\gamma} $$

  Da questo consegue che un corpo in moto appare accorciato lungo la direzione del suo movimento:

  $$ L = \frac{L'}{\gamma} $$

  Pertanto, la contrazione delle lunghezze non è un effetto dinamico, ma una conseguenza inevitabile della trasformazione spazio-temporale che lega i sistemi inerziali.

  Nota. È importante sottolineare che questa contrazione riguarda solo la direzione di moto, non riguarda le altre dimensioni perpendicolari al moto. Se l’oggetto possiede estensioni lungo gli assi ortogonali alla velocità (ad esempio lungo y oppure z), queste restano invariate, poiché le trasformazioni di Lorentz non modificano le coordinate spaziali trasversali.

• Dilatazione del tempo
  Un intervallo di tempo proprio $T′$ è la durata misurata nel sistema $S′$, dove l’orologio è a riposo (cioé dove si trova). Se il sistema $S′$ si muove rispetto a un altro sistema $S$, allora, dal punto di vista di un osservatore in $S$, il tempo in $S′$ scorre più lentamente: $$ T = \gamma T' $$

  Esempio. Un orologio segna $1$ secondo ($T'=1s$) nel suo sistema $ S' $ (astronave) che si muove al 90% della velocità della luce ($v=0.9c$). Dal punto di vista di chi osserva l'astronave da un sistema inerziale $ S $ più lento, il tempo dell'orologio in $ S' $ risulta più dilatato. $$ \gamma = \frac{1}{\sqrt{1-(0.9)^2}} \approx 2.29 $$ $$ T = \gamma T' \approx 2.29 \ s  $$ In altre parole, l’osservatore esterno vede le lancette dell’orologio a bordo dell’astronave muoversi più lentamente.
  

  Dimostrazione della dilatazione del tempo
  

  Considero un orologio in un sistema $ S' $, ad esempio un astronave in movimento o una particella.

  L'intervallo di tempo $ T' $ tra due "tic" dell'orologio (un secondo) si chiama "tempo proprio". In questo caso gli eventi sono i due tic dell’orologio.

  $$ T' = t'_B - t'_A $$

  Per una persona che viaggia nel sistema $ S' $ l'orologio è appeso al muro. Quindi, i due tic avvengono nello stesso posto (all’origine) a distanza temporale $T'$.

  Ora, ipotizziamo che una persona da un sistema inerziale $S$ più lento, ad esempio dalla Terra, veda il sistema $ S' $ (l'astronave) muoversi a grande velocità $v$. Come vede muoversi le lancette dell'orologio su $ S' $? Per saperlo devo calcolare il tempo in $ S $ con la trasformazione di Lorentz:

  $$ t = \gamma \left(t' + \frac{v}{c^2}x'\right), \qquad  \gamma = \frac{1}{\sqrt{1-v^2/c^2}}. $$

  Calcolo i tempi dei due tic dell'orologio dal punto di vista del sistema $S$:

  L’intervallo temporale tra i due tic in $S$ è

  $$ T = t_B - t_A = \gamma T' $$

  Poiché $\gamma \geq 1$ è maggiore di uno, si ha sempre $T \geq T'$. Questo significa che nel sistema $ S $ (Terra) che vede l'orologio muoversi con l'astronave, l'intervallo tra i due tic dura di più, $T=\gamma T'$.

  Questo dimostra che lo scorrere del tempo rallenta in un sistema in moto. 

  • Il primo tic $t'_A=0, $ nel punto $ x'_A=0$
  • Il secondo tic $t'_B=T' $ nel punto $ x'_B=0$
  • Il primo tic $t_A = \gamma (0 + \frac{v}{c^2}\cdot 0) = 0$
  • Il secondo tic $t_B = \gamma (T' + \frac{v}{c^2}\cdot 0) = \gamma T'$.
• Composizione relativistica delle velocità
  Nella relatività ristretta le velocità non si sommano più linearmente come in meccanica classica. Se un corpo ha velocità \(u'\) rispetto a un sistema di riferimento \(S'\), e questo sistema si muove con velocità \(v\) rispetto a un altro sistema \(S\), allora la velocità del corpo misurata in \(S\) non è \(u = u' + v\), ma segue la legge relativistica: $$ u = \frac{u' + v}{1 + \tfrac{u'v}{c^2}} $$ Il denominatore garantisce che il risultato resti sempre minore o uguale a \(c\), anche quando si sommano velocità molto elevate. Infatti, se nel sistema \(S'\) un corpo viaggia alla velocità della luce (\(u' = c\)), in qualunque altro sistema inerziale la sua velocità rimane comunque \(u = c\).   In questo modo, la formula assicura l’invarianza della velocità della luce e mostra come la regola galileiana \(u = u' + v\) sia valida solo per velocità molto più piccole della luce \( v \ll c\).
  
  

  Esempio. Se un proiettile viaggia a $u' = 0.9c$ su un treno che si muove a $v = 0.5c$, la velocità rispetto a terra non è $1.4c$, ma: $$ u = \frac{0.9c + 0.5c}{1 + \frac{0.9 \cdot 0.5}{1}} = \frac{1.4c}{1 + 0.45} = \frac{1.4c}{1.45} \approx 0.9655c $$

  Dimostrazione

  In meccanica classica, le velocità si compongono secondo la regola galileiana: se un corpo si muove con velocità \( u' \) rispetto a un sistema \( S' \), e quest’ultimo si muove con velocità \( v \) rispetto a un sistema \( S \), la velocità del corpo rispetto a \( S \) è semplicemente la somma

  $$ u = u' + v $$

  Tuttavia, questa legge di composizione è incompatibile con i principi della relatività ristretta, poiché violerebbe l’invarianza della velocità della luce. Infatti, se un oggetto in \( S' \) viaggiasse alla velocità della luce \( c \), sommando velocità secondo la regola classica si otterrebbe:

  $$ u = c + v > c $$

  Questo va in contraddizione con il postulato einsteiniano che assegna un valore costante alla velocità della luce \( c \) in tutti i sistemi inerziali. Le trasformazioni di Lorentz, invece, forniscono la formula corretta di composizione delle velocità.

  Ad esempio, considero una particella che si muove lungo l’asse \( x \) con velocità \( u' \) nel sistema \( S' \). Le coordinate dei suoi spostamenti soddisfano

  $$ u' = \frac{\Delta x'}{\Delta t'} $$

  Dal punto di vista del sistema \( S \), le trasformazioni di Lorentz per le differenze spaziali e temporali sono

  $$ \Delta x = \gamma (\Delta x' + v \Delta t'), $$ $$ \Delta t = \gamma \left( \Delta t' + \frac{v}{c^2}\Delta x' \right) $$

  Pertanto, la velocità nel sistema \( S \) risulta:

  $$ u = \frac{\Delta x}{\Delta t} = \frac{ \gamma (\Delta x' + v \Delta t')}{ \gamma ( \Delta t' + \tfrac{v}{c^2}\Delta x' )} = \frac{\Delta x' + v \Delta t'}{\Delta t' + \tfrac{v}{c^2}\Delta x'} $$

  Divido numeratore e denominatore per $ \Delta t' $ e sapendo che $ u'=\Delta x'/\Delta t' $ ottengo:

  $$ u = \frac{ \frac{ \Delta x' + v \Delta t' }{ \Delta t'  } }{ \frac{ \Delta t' + \tfrac{v}{c^2}\Delta x' }{ \Delta t'  } } = \frac{\dfrac{\Delta x'}{\Delta t'}+v}{1+\dfrac{v}{c^2}\dfrac{\Delta x'}{\Delta t'}} = \frac{u' + v}{1 + \tfrac{u'v}{c^2}} $$

  Questa legge relativistica di composizione conserva il limite superiore della velocità della luce, ponendo un limite invalicabile ai processi dinamici.

  $$ u = \frac{u' + v}{1 + \tfrac{u'v}{c^2}} $$

  Se infatti \( u' = c \), allora \( u = c \) per qualunque valore di \( v \). Analogamente, se entrambe le velocità sono inferiori a \( c \), la velocità composta rimane sempre inferiore a \( c \).

  $$ u = \frac{c + v}{1 + \tfrac{cv}{c^2}} = \frac{c + v}{1 + \tfrac{v}{c}}  = \frac{c + v}{1 + \tfrac{v}{c}} \cdot \frac{c}{c}  = \frac{c(c + v)}{c + v} = c$$

  Da ciò consegue che la velocità della luce è una costante universale e non può essere superata sommando moti relativi.

  Nota. È opportuno notare come, nel limite classico \( v \ll c \) e \( u' \ll c \), il denominatore si avvicini all’unità $ 1 + \tfrac{u'v}{c^2} \approx 1 $, e la formula relativistica si riduca alla legge galileiana \( u \simeq u' + v \). $$ u =  \frac{u' + v}{1 + \tfrac{u'v}{c^2}} = \frac{u' + v}{1 + 0 } = u'+v $$ Questo garantisce la coerenza della formula di Lorentz anche con la meccanica classica in regime non relativistico.

Geometria dello spazio-tempo

La relatività ristretta non descrive lo spazio e il tempo come entità indipendenti, ma come parti di un’unica struttura geometrica chiamata spazio-tempo.

Ogni evento, qualcosa che accade in un punto dello spazio in un certo istante, si rappresenta con quattro coordinate: le tre spaziali \( (x,y,z) \) e quella temporale moltiplicata per la velocità della luce ( ct ). Questo forma un quattro-vettore $(x, y, z, ct)$.

Le trasformazioni di Lorentz non cambiano la forma di una grandezza speciale che prende il nome di intervallo spazio-temporale:

\[  s^2 = c^2 t^2 - x^2 - y^2 - z^2 \]

Questo intervallo gioca nello spazio-tempo il ruolo che la distanza euclidea ha nello spazio ordinario. Ad esempio, nelle rotazioni tridimensionali la distanza non cambia, allo stesso modo nelle trasformazioni di Lorentz l’intervallo spazio-temporale non cambia, è un invariante.

In conclusione, le trasformazioni di Lorentz hanno modificato profondamente la visione classica del tempo e dello spazio, eliminando ogni nozione di assoluto.

Costituiscono il fondamento matematico e concettuale della relatività ristretta, e sono indispensabili per comprendere fenomeni ad alte velocità, come la fisica delle particelle, l’elettrodinamica relativistica e la cosmologia.

E così via.